Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-22T14:06:23.121Z Has data issue: false hasContentIssue false
  • English
  • Français

Metric Compactifications and Coarse Structures

Published online by Cambridge University Press:  20 November 2018

Kotaro Mine  and
Atsushi Yamashita
Kotaro Mine
Affiliation:
Graduate School of Mathematical Sciences,The University of Tokyo, Tokyo 153-8914, Japan. e-mail: [email protected]
Atsushi Yamashita
Affiliation:
Chiba Institute of Technology, 2-1-1, Shibazono, Narashino-shi, Chiba, 275-0023, Japan. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 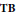$\mathbf{TB}$ be the category of totally bounded, locally compact metric spaces with the 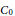${{C}_{0}}$ coarse structures. We show that if 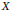$X$ and 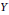$Y$ are in 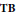$\mathbf{TB}$, then 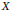$X$ and 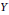$Y$ are coarsely equivalent if and only if their Higson coronas are homeomorphic. In fact, the Higson corona functor gives an equivalence of categories $\mathbf{TB}\,\to \,\mathbf{K}$, where 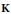$\mathbf{K}$ is the category of compact metrizable spaces. We use this fact to show that the continuously controlled coarse structure on a locally compact space 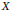$X$ induced by some metrizable compactification 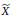$\widetilde{X}$ is determined only by the topology of the remainder 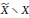$\widetilde{X}\,\backslash \,X$.

Keywords

18B3051F9953C2354C20coarse geometryHigson coronacontinuously controlled coarse structureuniformcontinuityboundary at infinity
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 5 , 01 October 2015 , pp. 1091 - 1108
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Engelking, R., General topology. Second ed., Sigma Series in Pure Mathematics, 6, Heldermann Verlag, Berlin, 1989.Google Scholar
[2] M. Bonk, and Schramm, O., Embeddings of Gromov hyperbolic spaces. Geom. Funct. Anal. 10(2000), no. 2, 266–306.http://dx.doi.org/10.1007/s000390050009 Google Scholar
[3] Bridson, M. R. and Haefliger, A. Metric spaces of non–positive curvature. Grundlehrender Mathematischen Wissenschaften, 319, Springer-Verlag, Berlin, 1999.Google Scholar
[4] Buyalo, S. and Schroeder, V., Elements of asymptotic geometry. EMS Monographs in Mathematics, European Mathematical Society (EMS), Zürich, 2007.Google Scholar
[5] Cuchillo-Ibáñfiez, E., Dydak, J., Koyama, A., and Moron, M. A., Co-coarse geometry of complements of Z-sets in the Hilbert cube. Trans. Amer. Math. Soc. 360(2008), no. 10, 5229–5246.http://dx.doi.Org/10.1090/S0002–9947–08–04603–5 Google Scholar
[6] Carlsson, G. and Pedersen, E. K., Controlled algebra and the Novikov conjectures for K- and L-theory. Topology 34(1995), no. 3, 731–758.http://dx.doi.org/10.1016/0040–9383(94)00033–H Google Scholar
[7] Higson, N., Pedersen, E. K., and Roe, J., C*-algebras and controlled topology. Jf-Theory 11(1997), no. 3, 209–239.http://dx.doi.Org/10.1023/A:1007705726771 Google Scholar
[8] Jordi, J., Interplay between interior and boundary geometry in Gromov hyperbolic spaces. Geom. Dedicata 149(2010), 129–154. http://dx.doi.org/10.1007/s10711–010–9472–0 Google Scholar
[9] Paulin, F., Un groupe hyperbolique est déterminé par son bord. J. London Math. Soc. (2) 54(1996), no. 1, 50–74.http://dx.doi.Org/10.1112/jlms/54.1.50 Google Scholar
[10] Roe, J., Lectures on coarse geometry. University Lecture Series, 31, American Mathematical Society, Providence, RI, 2003.Google Scholar
[11] Roe, J., Corrections to “Lectures on coarse geometry. http://www.personal.psu.edu/jxr57/writings/correction.pdf Google Scholar
[12] Rosenthal, D., Splitting with continuous control in algebraic K-theory. Jf-Theory 32(2004), no. 2,139–166.http://dx.doi.Org/10.1023/B:KTHE.0000037563.35102.0d Google Scholar
[13] Woods, R. G., The minimum uniform compactification of a metric space. Fund. Math. 147(1995), 39–59.Google Scholar
[14] Wright, N., Co coarse geometry and scalar curvature. J. Funct. Anal. 197(2003), no. 2, 469–488.http://dx.doi.org/10.1016/SOO22–1236(02)00025–3 Google Scholar