Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T00:39:19.013Z Has data issue: false hasContentIssue false
  • English
  • Français

The Method of Upper and Lower Solutions for Some Nonlinear Boundary Value Problems in Unbounded Domains

Published online by Cambridge University Press:  20 November 2018

Nguyên Phuong Các
Nguyên Phuong Các*
Affiliation:
The University of Iowa, Iowa City, Iowa
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let D be a bounded domain in the Euclidean space RN(N ≦ 2) and let 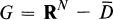where 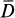is the closure of D. We assume that the boundary ∂G of G is smooth. Consider the boundary value problem (abbreviated to BVP in the sequel).

(1)

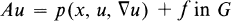
(1)

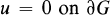
where A is a nonlinear elliptic differential operator in divergence form of Leray-Lions type, ∇u = grad u, f is a distribution on G and p(x, t, η) is a function defined on G × R × RN. Among other hypotheses we shall, roughly speaking, assume that p has completely unrelated growth rates in the first and the third variables. In this paper we prove the solvability of the BVP (1), (2) under the assumption that it has both an upper solution ψ and a lower solution φ with φ ≧ ψ.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 3 , 01 June 1985 , pp. 430 - 441
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Các, N. P., Nonlinear elliptic boundary value problems for unbounded domains, J. Differential Equations 45 (1982), 191–198.Google Scholar
2. Các, N. P., On some quasilinear elliptic boundary value problems with conditions at infinity, J. Differential Equations 52 (1984), 342–355.Google Scholar
3. Hess, P., Nonlinear elliptic problems in unbounded domains, International Summer School on Nonlinear Operators, Berlin, Sept. 1975, in “Abhandlung der Akademie der Wissenschafter der DDR.“Google Scholar
4. Hess, P., A second order nonlinear elliptic boundary value problem, in “Nonlinear Analysis: A collection of papers in honor of Erich H. Rothe,” (Academic Press, New York, 1978).CrossRefGoogle Scholar
5. Lions, J. L., Quelques méthodes de résolution des problèmes aux limites nonlinéaires (Dunod, Gauthier-Villars, Paris, 1969).Google Scholar