Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T01:00:53.383Z Has data issue: false hasContentIssue false
  • English
  • Français

Merotopic Spaces and Extensions of Closure Spaces

Published online by Cambridge University Press:  20 November 2018

K. C. Chattopadhyay ,
Olav Njåstad  and
W. J. Thron
K. C. Chattopadhyay
Affiliation:
Burdwan University, Burdwan, West Bengal, India
Olav Njåstad
Affiliation:
University of Trondheim-NTH, Trondheim, Norway
W. J. Thron
Affiliation:
University of Colorado, Boulder, Boulder, Colorado
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Proximity spaces and contiguity spaces, and more recently nearness spaces, have been studied not just because they provide various approaches to uniform structure. Possibly of greater importance is that they can be used as a means of introducing compactifications and more general extensions of the topological spaces on which they are defined. Riesz [20] was probably the first to recognize this connection. Since then the idea was used by Freudenthal [9], Alexandroff [1], Smirnov [21], Leader [17] and Ivanov and Ivanova [13, 14, 15] among others.

Recently Reed [19] using work of Bentley [2, 4] and Herrlich [11, 12] studied the 1 – 1 correspondence between the class 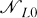of all cluster generated nearness spaces and the class 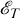all principal T1-extensions of a given T1-space. She succeeded in showing that the mapping induces a 1 – 1 correspondence between the contingual nearness spaces in 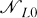and the compactifications in .

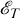Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 4 , 01 August 1983 , pp. 613 - 629
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Alexandroff, P., Bicompact extensions of topological spaces, Mat. Sb. 5 (1939), 403–424.Google Scholar
2. Bentley, H. L., Nearness spaces and extensions of topological spaces, Studies in Topology (New York, 1975), 47–66.Google Scholar
3. Bentley, H. L., The role of nearness spaces in topology, Categorical Topology, Lecture Notes in Mathematics 540 (Springer-Verlag, Berlin, 1976), 1–22.Google Scholar
4. Bentley, H. L. and Herrlich, H., Extensions of topological spaces. Proceedings of the Memphis State Univ. Conference in Topology (1975), 129–184.Google Scholar
5. Bentley, H. L. and Herrlich, H., The forgetful functor Cont → Prox is topological, Quaestiones Mathematicae 2 (1977), 45–57.Google Scholar
6. Cech, E., Topological spaces. Revised ed. (Praha, 1966).Google Scholar
7. Chattopadhyay, K. C. and Thron, W. J., Extensions of closure spaces, Can. J. Math. 20 (1977), 1277–1286.Google Scholar
8. Choquet, G., Sur les notions de filtre et de grille, Comptes Rendus Acad. Sci. Paris 224 (1947), 171–173.Google Scholar
9. Freudenthal, H., Neuaufbau der Endentheorie, Ann. Math 43 (1942), 261–279.Google Scholar
10. Gagrat, M. and Thron, W. J., Nearness structures and proximity extensions, Trans. Amer. Math. Soc. 208 (1975), 103–125.Google Scholar
11. Herrlich, H., A concept of nearness, Gen. Top. Appl. 4 (1974), 191–212.Google Scholar
12. Herrlich, H., Topological structures, Math. Centre Tracts 52 (1974), 59–122.Google Scholar
13. Ivanova, V. M. and Ivanov, A. A., Contiguity spaces and bicompact extensions, Izo. Akad. Nauk. SSSR 12 (1959), 613–634.Google Scholar
14. Ivanova, V. M. and Ivanov, A. A., Contiguity spaces and bicompact extensions of topological spaces, Dokl. Akad. Nauk SSSR 127 (1959), 20–22.Google Scholar
15. Ivanov, A. A., Regular extensions of topological spaces, Contrib. Ext. Theory. Top. Struc. Berlin (1969), 133–138.Google Scholar
16. Katětov, M., On continuity structures and spaces of mappings, Comm. Math. Univ. Carolinae 6 (1965), 257–278.Google Scholar
17. Leader, S., On clusters in proximity spaces, Fund. Math. 47 (1959), 205–213.Google Scholar
18. Naimpally, S. and Whitfield, J. H. M., Not every family is contained in a clan, Proc. Amer. Math. Soc. 47 (1975), 237–238.Google Scholar
19. Reed, E. E., Nearnesses, proximities and T1-compactifications, Trans. Amer. Math. Soc. 236 (1978), 193–207.Google Scholar
20. Riesz, F., Stetigkeitsbegriff und abstrakte Mengenlehre, Atti IV Congr. Intern. Math. Roma (1908), 18–24.Google Scholar
21. Smirnov, J. M., On proximity spaces, Mat. Sb 31 (1952), 543–574. English Translation, Amer. Math. Soc. Transi. 38 (1964), 5–35.Google Scholar
22. Thron, W. J., Proximity structures and grills, Math. Ann. 206 (1973), 35–62.Google Scholar