Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T00:42:07.220Z Has data issue: false hasContentIssue false
  • English
  • Français

The Measure Spectrum of a Uniform Algebra and Subharmonicity

Published online by Cambridge University Press:  20 November 2018

Donna Kumagai
Donna Kumagai*
Affiliation:
The Pennsylvania State University, Reading, Pennsylvania
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be a uniform algebra on a compact Hausdorff space X. The spectrum, or the maximal ideal space, MA, of A is given by

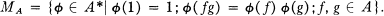
We define the measure spectrum, SA, of A by

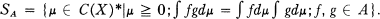
SA is the set of all representing measures on X for all Φ ∈ MA. (A representing measure for Φ ∈ MA is a probability measure μ on X satisfying

The concept of representing measure continues to be an effective tool in the study of uniform algebras. See for example [12, Chapters 2 and 3], [5, pp. 15-22] and [3]. Most of the known results on the subject of representing measures, however, concern measures associated with a single homomorphism.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 3 , 01 June 1982 , pp. 673 - 685
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. Ahern, P. R., On the geometry of the unit ball in the space of real annihilating measures, Pac. J. Math. 28 (1969), 1–7.Google Scholar
2. Aupetit, B., Propriétés spectrales des algebres de Banach 735 (Springer-Verlag, 1979.Google Scholar
3. Gamelin, T. W., Uniform algebras and Jensen measures (Cambridge University Press, Cambridge, 1978.Google Scholar
4. Gamelin, T. W., Uniform algebras (Prentice Hall, 1969.Google Scholar
5. Glicksberg, I., Recent results on function algebras (American Mathematical Society, Providence, R.I., 1972.Google Scholar
6. Helms, L. L., Introductions to potential theory (Wiley Interscience, N.Y., 1969), 68.Google Scholar
7. Kumagai, D., Subharmonic functions and uniform algebras, Proceedings AMS 78 (1980), 23–29.Google Scholar
8. Nehari, Z., Conformai mapping (McGraw Hill, N.Y., 1952.Google Scholar
9. Royden, H., The boundary values of analytic and subharmonic functions, Math. Z. 78 (1962).Google Scholar
10. Senickin, V. N., Subharmonic functions and analytic structure in the maximal ideal space of a uniform algebra, Math. USSR Sbornik 36 (1980).Google Scholar
11. Slodkowski, Z., On subharmonicity of the capacity of the spectrum, Proc. Amer. Math. Soc, to appear.Google Scholar
12. Stout, E. L., The theory of uniform algebras (Bogden and Quigley, Tarrytown-on- Hudson, N.Y., 1971.Google Scholar
13. Wermer, J., Banach algebras and analytic functions, Advances in Math. 1 (1961), 51–102.Google Scholar
14. Wermer, J., Banach algebras and several complex variables (Springer-Verlag, 1976.Google Scholar
15. Wermer, J., Subharmonicity and hulls, Pac. J. Math. 8 (1975), 283–290.Google Scholar