Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T09:31:29.944Z Has data issue: false hasContentIssue false
  • English
  • Français

Mean Value and Limit Theorems for Generalized Matrix Functions

Published online by Cambridge University Press:  20 November 2018

Paul J. Nikolai
Paul J. Nikolai*
Affiliation:
Aerospace Research Laboratories (OAR), Wright-Patterson Air Force Base, Ohio;
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A = [aij] denote an n-square matrix with entries in the field of complex numbers. Denote by H a subgroup of Sn, the symmetric group on the integers 1, …, n, and by 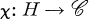a character of degree 1 on H. Then

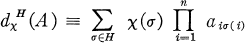
is the generalized matrix function of A associated with H and x; e.g., if H = Sn and χ = 1, then 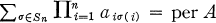the permanent function. If the sequences ω = (ω1, …, ωm) and ϒ = (ϒ1, …, ϒm) are m-selections, m ≦ w, of integers 1, …, n, then A [ω| ϒ] denotes the m-square generalized submatrix [aωiϒj], i, j = 1, …, m, of the n-square matrix A. If ω is an increasing m-combination, then A [ω|ω] is an m-square principal submatrix of A.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 982 - 991
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Beckenbach, Edwin F. and Bellman, Richard, Inequalities, Chapter I (Springer, Berlin, 1961).Google Scholar
2. Brualdi, Richard A., On the permanent and maximal characteristic root of a non-negative matrix, Proc. Amer. Math. Soc. 17 (1986), 1413–1416.Google Scholar
3. Cargo, G. T. and Shisha, O., Bounds on ratios of means, J. Res. Nat. Bur. Standards 66B (1962), 169–170.Google Scholar
4. Greub, W. H., Multilinear algebra (Springer, New York, 1967).Google Scholar
5. Hardy, G. H., Littlewood, J. E., and G. Pôlya, Inequalities, 2nd éd., Chapter II (Cambridge Univ. Press, London, 1952).Google Scholar
6. Marcus, Marvin, On two classical results of I. Schur, Bull. Amer. Math. Soc. 70 (1964), 685–688.Google Scholar
7. Marcus, Marvin, Matrix applications of a quadratic identity for decomposable symmetrized tensors, Bull. Amer. Math. Soc. 71 (1965), 360–364.Google Scholar
8. Marcus, Marvin, Lengths of tensors, pp. 163-176 of Inequalities, Proceedings of a Symposium, Wright-Patterson Air Force Base, Ohio, 1965, edited by O., Shisha (Academic Press, New York, 1967).Google Scholar
9. Marcus, Marvin and Khan, N. A., Some generalizations of Kantorovich's inequality, Portugal. Math. 20 (1961), 33–38.Google Scholar
10. Marcus, Marvin and McGregor, J. L., Extremal properties of hermitian matrices, Can. J. Math. 8 (1956), 524–531.Google Scholar
11. Marcus, Marvin and Mine, Henryk, A survey of matrix theory and matrix inequalities (Allyn and Bacon, Boston, 1964).Google Scholar
12. Marcus, Marvin and Mine, Henryk, Generalized matrix functions, Trans. Amer. Math. Soc. 116 (1965), 316–329.Google Scholar
13. Marcus, Marvin and Newman, Morris, Inequalities for the permanent function, Ann. of Math. (2) 75 (1962), 47–62.Google Scholar
14. Schur, I., Über endliche Gruppen und Hermitesche Formen, Math. Z. 1 (1918), 184–207.Google Scholar
15. Shisha, O. and Mond, B., Bounds on differences of means, pp. 293-308 of Inequalities, Proceedings of a Symposium, Wright-Patterson Air Force Base, Ohio, 1965, edited by Shisha, O. (Academic Press, New York, 1967).Google Scholar
16. Shniad, Harold, On the convexity of mean value functions, Bull. Amer. Math. Soc. 54 (1948), 770–776.Google Scholar