Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T01:06:46.316Z Has data issue: false hasContentIssue false
  • English
  • Français

The Maximal p-Extension of a Local Field

Published online by Cambridge University Press:  20 November 2018

Murray A. Marshall
Murray A. Marshall*
Affiliation:
University of Saskatchewan, Saskatoon, Saskatchewan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Let k denote a local field, that is, a complete discrete-valued field with perfect residue class field 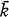. Let G denote the Galois group of the maximal separable algebraic extension M of k, and let g denote the corresponding object over 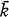. For a given prime integer p, let G(p) denote the Galois group of the maximal p-extension of k. The dimensions of the cohomology groups

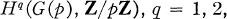
considered as vector spaces over the prime field Z/pZ, are equal, respectively, to the rank and the relation rank of the pro-p-group G(p); see [4; 9]. These dimensions are well known in many cases, especially when k is finite [6; 3; (Hoechsmann) 2, pp. 297-304], but also when k has characteristic p, or when k contains a primitive pth root of unity [4, p. 205].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 23 , Issue 3 , June 1971 , pp. 398 - 402
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Artin, E. and Tate, J., Class field theory (Benjamin, New York, 1967).Google Scholar
2. Cassels, J. W. S. and A. Froehlich, Algebraic number theory (Thompson Book Co., Washington, D.C., 1967).Google Scholar
3. Demuskin, S. P., The group of a maximal p-extension of a local field, Izv. Akad. Nauk SSSR Ser. Mat. 25 (1961), 329–346.Google Scholar
4. Lang, S., Rapport sur la cohomologie des groupes (Benjamin, New York, 1966).Google Scholar
5. Marshall, M. A., The ramification filters of abelian extensions of a local field, Queen's University Preprint 1969-6, Kingston, Ontario.Google Scholar
6. Safarevic, I. R., Onp-extensions, Mat. Sb. (N.S.) 20 (62), (1947), 351–363.Google Scholar
7. Serre, J.-P., Corps locaux (Hermann, Paris, 1962).Google Scholar
8. Serre, J.-P., Sur les corps locaux à corps résiduel algébricquement clos, Bull. Soc. Math. France 89 (1961), 105–154.Google Scholar
9. Serre, J.-P., Cohomologie galoisienne (Springer-Verlag, Berlin, 1965).Google Scholar
10. Wyman, B. F., Wildly ramified gamma extensions, Amer. J. Math. 91 (1969), 135–152.Google Scholar