Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Henriksen, M.
Vermeer, J.
and
Woods, R. G.
1987.
Quasi 𝐹-covers of Tychonoff spaces.
Transactions of the American Mathematical Society,
Vol. 303,
Issue. 2,
p.
779.
Zaharov, V. K.
1988.
On functions connected with sequential absolute, cantor completion and classical ring of quotients.
Periodica Mathematica Hungarica,
Vol. 19,
Issue. 2,
p.
113.
Conrad, Paul
and
Martinez, Jorge
1990.
Complemented lattice-ordered groups.
Indagationes Mathematicae,
Vol. 1,
Issue. 3,
p.
281.
Hager, A. W.
and
Martinez, Jorge
1992.
Fraction-dense algebras and spaces.
Acta Applicandae Mathematicae,
Vol. 27,
Issue. 1-2,
p.
55.
Hager, A. W.
and
Martinez, Jorge
1992.
Positive Operators and Semigroups on Banach Lattices.
p.
55.
Hager, Anthony W.
and
Martinez, Jorge
1993.
Fraction-Dense Algebras and Spaces.
Canadian Journal of Mathematics,
Vol. 45,
Issue. 5,
p.
977.
Henriksen, Melvin
Larson, Suzanne
Martinez, Jorge
and
Woods, R. G.
1994.
Lattice-ordered algebras that are subdirect products of valuation domains.
Transactions of the American Mathematical Society,
Vol. 345,
Issue. 1,
p.
195.
Vechtomov, E. M.
1995.
Rings and sheaves.
Journal of Mathematical Sciences,
Vol. 74,
Issue. 1,
p.
749.
Zakharov, V. K.
1995.
Classical extensions of the ring of continuous functions and the corresponding preimages of a completely regular space.
Journal of Mathematical Sciences,
Vol. 73,
Issue. 1,
p.
114.
Henriksen, Melvin
1997.
Ordered Algebraic Structures.
p.
1.
Martínez, Jorge
2002.
Ordered Algebraic Structures.
Vol. 7,
Issue. ,
p.
89.
Hager, Anthony W.
and
Martinez, Jorge
2003.
α-Specker spaces.
Topology and its Applications,
Vol. 131,
Issue. 1,
p.
57.
Martinez, Jorge
2004.
Polar functions—II: completion classes of archimedean f-algebras vs. covers of compact spaces.
Journal of Pure and Applied Algebra,
Vol. 190,
Issue. 1-3,
p.
225.
Hager, Anthony W.
and
Martínez, Jorge
2007.
Patch-generated Frames and Projectable Hulls.
Applied Categorical Structures,
Vol. 15,
Issue. 1-2,
p.
49.
Bhattacharjee, Papiya
and
McGovern, Warren Wm.
2018.
Maximal d-subgroups and ultrafilters.
Rendiconti del Circolo Matematico di Palermo Series 2,
Vol. 67,
Issue. 3,
p.
421.
Bhattacharjee, Papiya
2019.
Maximal d-Elements of an Algebraic Frame.
Order,
Vol. 36,
Issue. 2,
p.
377.
Ruan, Xianglong
2024.
The d-elements of precoherent preidempotent quantales and their applications.
Logic Journal of the IGPL,
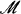 of minimal prime ideals and the space
of minimal prime ideals and the space 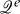 of all e-maximal ideals in L (where e > 0 is a weak order unit).
of all e-maximal ideals in L (where e > 0 is a weak order unit).