Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Stieglitz, Michael
1973.
Matrixtransformationen von unvollst�ndigen Folgenr�umen.
Mathematische Zeitschrift,
Vol. 133,
Issue. 2,
p.
129.
Kangro, G. F.
1976.
Theory of summability of sequences and series.
Journal of Soviet Mathematics,
Vol. 5,
Issue. 1,
p.
1.


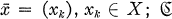 for the set of Cauchy sequences; and
for the set of Cauchy sequences; and 