Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-25T21:14:57.716Z Has data issue: false hasContentIssue false
  • English
  • Français

Matrices with Elements in a Boolean Ring

Published online by Cambridge University Press:  20 November 2018

A. T. Butson
A. T. Butson*
Affiliation:
University of Florida
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Introduction. Let 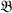be a Boolean ring of at least two elements containing a unit 1. Form the set 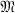of matrices A, B, … of order n having entries aiJ, bij, … (i, j = 1, 2, …, n), which are members of 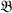. A matrix U of 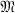is called unimodular if there exists a matrix V of 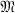such that VU= I, the identity matrix. Two matrices A and B are said to be left-associates if there exists a unimodular matrix U satisfying UA = B.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 9 , 1957 , pp. 47 - 59
Copyright
Copyright © Canadian Mathematical Society 1957

References

1. Bell, B. T., Arithmetic of logic, Trans. Amer. Math. Soc, 29 (1927), 597–611.Google Scholar
2. Birkhoff, G., Lattice Theory, Amer. Math. Soc. Colloq. Publ., 25 (rev. ed., New York, 1948).Google Scholar
3. Kaplansky, I., Elementary divisors and modules, Trans. Amer. Math. Soc, 66 (1949), 464–491.Google Scholar
4. MacDuffee, C. C., Matrices wivh elements in a principal ideal ring, Bull. Amer. Math. Soc, 39 (1933), 564–584.Google Scholar
5. Steinitz, E., Rechteckige Systeme und Moduln in algebraischen Zahlkörpern, Math. Ann., 71 (1911), 328–354, and 72 (1912), 297–345.Google Scholar
6. Stewart, B. M., A note on least common left multiples, Bull. Amer. Math. Soc, 55 (1949), 587–591.Google Scholar