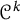 $\mathcal {C}^k$-seeley-extension-theorem for Bastiani’s differential calculus
$\mathcal {C}^k$-seeley-extension-theorem for Bastiani’s differential calculusPublished online by Cambridge University Press: 20 October 2021
We generalize a classical extension result by Seeley in the context of Bastiani’s differential calculus to infinite dimensions. The construction follows Seeley’s original approach, but is significantly more involved as not only
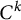 $C^k$
-maps (for
$C^k$
-maps (for
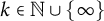 ) on (subsets of) half spaces are extended, but also continuous extensions of their differentials to some given piece of boundary of the domains under consideration. A further feature of the generalization is that we construct families of extension operators (instead of only one single extension operator) that fulfill certain compatibility (and continuity) conditions. Various applications are discussed as well.
) on (subsets of) half spaces are extended, but also continuous extensions of their differentials to some given piece of boundary of the domains under consideration. A further feature of the generalization is that we construct families of extension operators (instead of only one single extension operator) that fulfill certain compatibility (and continuity) conditions. Various applications are discussed as well.