Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T00:38:23.140Z Has data issue: false hasContentIssue false
  • English
  • Français

Massey Products and Lower Central Series of Free Groups

Published online by Cambridge University Press:  20 November 2018

Roger Fenn  and
Denis Sjerve
Roger Fenn
Affiliation:
University of British Columbia, Vancouver, British Columbia
Denis Sjerve
Affiliation:
University of British Columbia, Vancouver, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of this paper is to continue the investigation into the relationships amongst Massey products, lower central series of free groups and the free differential calculus (see [4], [9], [12]). In particular we set forth the notion of a universal Massey product ≪α1, …, αk≫, where the αi are one dimensional cohomology classes. This product is defined with zero indeterminacy, natural and multilinear in its variables.

In order to state the results we need some notation. Throughout F will denote the free group on fixed generators x1, …, xn and

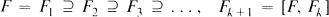
will denote the lower central series of F. If I = (i1, …, ik) is a sequence such that 1 ≦ i1, …, ik ≦ n then ∂1 is the iterated Fox derivative and 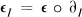, where 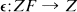is the augmentation. By convention we set ∂1 = identity if I is empty.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 2 , 01 April 1987 , pp. 322 - 337
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Dwyer, , Homology, Massey products and maps between groups. Journal of Pure and Applied Algebra 6 (1975), 177–190.Google Scholar
2. Dyer-Vasquez, , Some small aspherical spaces, Jour. Australian Math. Soc. 16 (1973), 332–352.Google Scholar
3. Fenn-Sjerve, , Duality and cohomology for one relator groups, Pacific J. Math. 103 (1982), 365–375.Google Scholar
4. Fenn-Sjerve, , Basic commutators and minimal Massey products, Can. J. Math. 36 (1984), 1119–1146.Google Scholar
5. Labute, , Classification of Demushkin groups, Can. J. Math. 19 (1967), 106–121.Google Scholar
6. Lyndon, , Cohomology theory of groups with a single defining relation, Annals of Math. 52 (1950), 650–665.Google Scholar
7. MacLane, , Homology (Springer-Verlag, 1963).CrossRefGoogle Scholar
8. May, , Matric Massey products, Jour. Alg. 12 (1969), 533–568.Google Scholar
9. Porter, , Milnor's -invariants and Massey products, T.A.M.S. 257 (1980), 39–71.Google Scholar
10. Ratcliffe, , On one relator groups which satisfy Poincaré duality, Math. Z. 177 (1981), 425–438.Google Scholar
11. Shapiro-Sonn, , Free factor groups of one relator groups, Duke Math. J. 41 (1974), 83–88.Google Scholar
12. Turaev, , The Milnor invariants and Massey products, Studies in Topology II, Zap. Nanc. Sem. Lenin. Of. Mat. Kogo in Stet. Acad. Nauk SSSR 66 (1976), 189–203.Google Scholar