Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T06:54:55.288Z Has data issue: false hasContentIssue false
  • English
  • Français

Maps Preserving Complementarity of Closed Subspaces of a Hilbert Space

Published online by Cambridge University Press:  18 June 2019

Lucijan Plevnik  and
Peter Šemrl
Lucijan Plevnik
Affiliation:
Institute of Mathematics, Physics, and Mechanics, Jadranska 19, SI-1000 Ljubljana, Slovenia. e-mail: [email protected]
Peter Šemrl
Affiliation:
Faculty of Mathematics and Physics, University of Ljubljana, Jadranska 19, SI-1000 Ljubljana, Slovenia. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 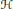$\mathcal{H}$ and 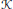$\mathcal{K}$ be infinite-dimensional separable Hilbert spaces and 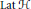$\text{Lat}\,\mathcal{H}$ the lattice of all closed subspaces oh 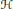$\mathcal{H}$. We describe the general form of pairs of bijective maps 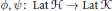$\phi ,\,\psi :\,\text{Lat}\,\mathcal{H}\,\to \,\text{Lat}\,\mathcal{K}$ having the property that for every pair 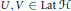$U,\,V\,\in \,\text{Lat}\,\mathcal{H}$ we have 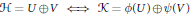$\mathcal{H}\,=\,U\,\oplus \,V\,\Leftrightarrow \,\mathcal{K}\,=\,\phi \left( U \right)\,\oplus \,\psi \,\left( V \right)$. Then we reformulate this theorem as a description of bijective image equality and kernel equality preserving maps acting on bounded linear idempotent operators. Several known structural results for maps on idempotents are easy consequences.

Keywords

46B2047B49Hilbert spacelattice of closed subspacescomplemented subspacesadjacent subspacesidempotents
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 5 , 01 October 2014 , pp. 1143 - 1166
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1]Blunck, A. and Havlicek, H., On bijections that preserve complementarity of subspaces. Discrete Math. 301(2005), no. 1, 46–56 http://dx.doi.org/10.1016/j.disc.2004.11.018.Google Scholar
[2] Chan, J.-T., C.-K. Li, N.-S., Sze, Mappings preserving spectra of product of matrices. Proc. Amer. Math. Soc. 135(2007), no. 4, 977–986 http://dx.doi.org/10.1090/S0002-9939-06-08568-6.Google Scholar
[3]Chow, W.-L., On the geometry of algebraic homogeneous spaces. Ann. of Math. 50(1949), 32–67 http://dx.doi.org/10.2307/1969351.Google Scholar
[4] Faure, C. A., An elementary proof of the fundamental theorem of projective geometry. Geom. Dedicata 90(2002), 145–151 http://dx.doi.org/10.1023/A:1014933313332.Google Scholar
[5] Fillmore, P. A. and Longstaff, W. E., On isomorphisms of lattices of closed subspaces. Canad. J. Math. 36(1984), no. 5, 820–829 http://dx.doi.org/10.4153/CJM-1984-048-x.Google Scholar
[6] Giol, J., Segments of bounded linear idempotents on a Hilbert space. J. Funct. Anal. 229(2005), no. 2, 405–423 http://dx.doi.org/10.1016/j.jfa.2005.03.017.Google Scholar
[7] Li, C.-K. and Pierce, S., Linear preserver problem. Amer. Math. Monthly 108(2001), no. 7, 591–605 http://dx.doi.org/10.2307/2695268.Google Scholar
[8]Lin, Y.-F. and Wong, T.-L., A note on 2-local maps. Proc. Edinb. Math. Soc. 49(2006), no. 3, 701–708 http://dx.doi.org/10.1017/S0013091504001142.Google Scholar
[9] Lindenstrauss, J. and Tzafriri, L., On the complemented subspaces problem. Israel J. Math. 9(1971), 263–269 http://dx.doi.org/10.1007/BF02771592.Google Scholar
[10] Mackey, G.W., Isomorphisms of normed linear spaces. Ann. of Math. 43(1942), 244–260 http://dx.doi.org/10.2307/1968868.Google Scholar
[11] Ovchinnikov, P. G., Automorphisms of the poset of skew projections. J. Funct. Anal. 115(1993), no. 1, 184–189 http://dx.doi.org/10.1006/jfan.1993.1086.Google Scholar
[12] Petek, T., Mappings preserving the idempotency of products of operators. Linear Multilinear Algebra 58(2010), no. 7–8, 903–925 http://dx.doi.org/10.1080/03081080903132593.Google Scholar