Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T00:32:21.739Z Has data issue: false hasContentIssue false
  • English
  • Français

The Map SJ → SF Does Not Deloop Mod 2

Published online by Cambridge University Press:  20 November 2018

Robert R. Clough
Robert R. Clough*
Affiliation:
Burroughs Corporation, Chicago, Illinois
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It has been widely conjectured that there exists a homotopy commutative Diagram

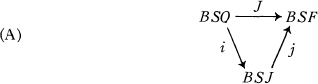
where J is the stable Whitehead f-homomorphism and BSJ is the space constructed in [3]. In [4], Stasheff and the author proved that this conjecture is false. However, Quillen's proof of the Adams conjecture in [7] has as a corollary the existence of the homotopy commutative diagram

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 4 , 01 August 1975 , pp. 737 - 745
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Adams, J. F., On the groups J(X), IV, Topology 5 (1966), 21–71.Google Scholar
2. Adams, J. F. and Walker, G., On Complex Stiefel manifolds, Proc. Cambridge Philos. Soc. 61 (1965), 81–103.Google Scholar
3. Clough, Robert R., T/je Z2-cohomology of a candidate for BImU), Illinois J. Math. 14 (1970), 424–433.Google Scholar
4. Clough, Robert R. and Stasheff, James D., BSJ does not map correctly into BSF mod 2, Manuscripta Math. 7 (1972), 205–214.Google Scholar
5. Milgram, R. J., Iterated loop spaces, Ann. of Math. 84 (1966), 386–403.Google Scholar
6. Moore, J. C., Algebra homologique et homologie des espaces classifiants, Séminaire Henri Cartan, 1959–1960. Exp. 7.Google Scholar
7. Quillen, Daniel, The Adams conjecture (to appear).Google Scholar
8. Rothenberg, M. and Steenrod, N., The cohomology of classifying spaces of H-spaces, Bull. Amer. Math. Soc. 71 (1965), 872–875.Google Scholar
9. Sullivan, Dennis, Geometric topology, I: Localization, periodicity, and Galois symmetry, M. I. T., Cambridge, Mass., 1970 (mimeographed notes).Google Scholar
10. Wu, W. T., Les i-carres dans une variété grassmannienne, C. R. Acad. Sci. Paris Sér. A-B 230 (1950), 918–920.Google Scholar