Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-19T22:06:49.969Z Has data issue: false hasContentIssue false
  • English
  • Français

The Manifold of Conformally Equivalent Metrics

Published online by Cambridge University Press:  20 November 2018

Arthur E. Fischer  and
Jerrold E. Marsden
Arthur E. Fischer
Affiliation:
University of California, Santa Cruz and Berkeley, California
Jerrold E. Marsden
Affiliation:
University of California, Santa Cruz and Berkeley, California
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

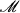Ebin [8] gives a thorough study of the space of riemannian metrics on a compact manifold M and of the action of the diffeomorphism group 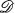of M on 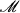. The purpose of this paper is to study the action of the larger group 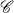of conformorphisms, or conformai transformations, on 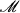and 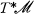on . On 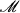, the L2-orthogonal decomposition induced by the action of 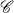gives a splitting of symmetric tensors into three summands introduced by York [25; 26]. We find submanifolds of 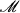tangent to the pieces of this decomposition.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 29 , Issue 1 , 01 February 1977 , pp. 193 - 209
Copyright
Copyright © Canadian Mathematical Society 1977

Footnotes

The research of the second author was partially supported by NSF Grant MPS-75-05576 and the Samuel Beatty Fund of the University of Toronto.

References

1. Agmon, S., A. Douglis and Nirenberg, L., Estimates near the boundary for solutions of elliptic partial differential equations satisfying general boundary conditions, II, Comm. Pure Appl. Math. 7 (1964), 35–92.Google Scholar
2. Arms, J., A. Fischer and Marsden, J., Une approche symplectique pour des théorèmes de composition en géométrie ou relativité générale, C. R. Acad. Sci. 281 (1975), 517–520.Google Scholar
3. Berger, M. and Ebin, D., Some decompositions of the space of symmetric tensors on a Riemannian manifold, J. Differential Geometry 3 (1969), 379–392.Google Scholar
4. Bourguignon, J. P., D. G. Ebin and Marsden, J. E., Sur le noyau des opérateurs pseudodifférentiels à symbole surjective et non-injective. C. R. Acad. Sci. 282 (1976), 867–870.Google Scholar
5. Cantor, M., Spaces of functions with asymptotic conditions on Rn, Indiana Univ. Math. J. 24 (1975), 897–902.Google Scholar
5. Cantor, M. Some problems of global analysis over asymptotically simple spaces, (preprint).Google Scholar
7. Chernoff, P. and Marsden, J., Some properties of infinite dimensional hamiltonian systems, Springer Lecture Notes 425 (1974).10.1007/BFb0073665CrossRefGoogle Scholar
8. Ebin, D. G., The manifold of Riemannian metrics, Proc. Symp. Pure Math. 15, Amer. Math. Soc. (1970), 11-40 and Bull. Amer. Math. Soc. 74 (1968), 1002–1004.Google Scholar
9. Ebin, D. and Marsden, J., Groups of diffeomorphisms and the motion of an incompressible fluid, Ann. of Math. 92 (1970), 102–163.Google Scholar
10. Fischer, A., The theory of super space, in Relativity, Carmeli, M., Fickler, S. and Witten, L. eds. (Plenum, 1967).Google Scholar
11. Fischer, A. and Marsden, J., The Einstein equations of evolution, a geometric approach, J. Math. Phys. 13 (1972), 546–568.Google Scholar
12. Fischer, A. and Marsden, J. Linearization stability of non-linear partial differential equations, Proc. Symp. Pure Math. Amer. Math. Soc. 27 (1974), 219–263.Google Scholar
13. Fischer, A. and Marsden, J. Deformations of the scalar curvature, Duke Math. Journal 4 (1975), 519–547.Google Scholar
14. Fischer, A. and Marsden, J. The space of true gravitational degrees of freedom, (in preparation).Google Scholar
15. Friedman, A., Partial differential equations (Holt, 1969).Google Scholar
16. Hôrmander, L., Pseudo-differential operators and non-elliptic boundary problems, Ann. of Math. 83 (1966), 129–209.Google Scholar
17. Kobayashi, S., Transformation groups in Riemannian geometry (Springer, 1973).Google Scholar
18. Kohn, J. J. and Nirenberg, L., Non-coercive boundary value problems, Comm. Pure and Appl. Math. 18 (1965), 443–492.Google Scholar
19. Lang, S., Differential manifolds (Addison-Wesley, Reading, Mass., 1972).Google Scholar
20. Marsden, J. and Weinstein, A., Reduction of symplectic manifolds with symmetry, Rep. on Math. Phys. 5 (1974), 121–130.Google Scholar
21. Moncrief, V., Decompositions of gravitational perturbations, J. Math. Phys. 16 (1975), 1556- 1560.Google Scholar
22. Murchadha, N. O. and York, J. W., Initial-value problem of general relativity. I. General formulation and physical interpretation, and 77. Stability of solutions of the initial-value equations, Phys. Rev. D. 10 (1974), 428-436 and 437–446.Google Scholar
23. Palais, R., Seminar on the Atiyah-Singer index theorem, Princeton, 1965.CrossRefGoogle Scholar
24. Wolf, J. A., Spaces of constant curvature, 3rd ed. (Publish or Perish, Boston, Mass., 1974).Google Scholar
25. York, J. W., Conformally invariant orthogonal decomposition of symmetric tensors on Riemannian manifolds and the initial value problem of general relativity, J. Mathematical Phys. 14 (1973), 456–464.Google Scholar
26. York, J. W. Covariant decompositions of symmetric tensors in the theory of gravitation, Ann. Inst. H. Poincaré, 21 (1974), 319–332 Google Scholar