Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-05T03:36:47.419Z Has data issue: false hasContentIssue false
  • English
  • Français

A Lower Bound For KxL Of Quasi-Polarized Surfaces (X, L) With Non-Negative Kodaira Dimension

Published online by Cambridge University Press:  20 November 2018

Yoshiaki Fukuma
Yoshiaki Fukuma*
Affiliation:
Department of Mathematics, Faculty of Science, Tokyo Institute of Technology, Oh-okayama, Meguro-ku, Tokyo 152-8551, Japan, [email protected]
*
Current address: Department of Mathematics, College of Education, Naruto University of Education, Takashima, Naruto-cho, Naruto-shi 772-8502, Japan email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 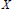$X$ be a smooth projective surface over the complex number field and let $L$ be a nef-big divisor on 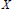$X$. Here we consider the following conjecture; If the Kodaira dimension 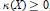$\kappa (X)\ge 0$, then 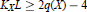${{K}_{X}}L\,\ge \,2q(X)\,-\,4$, where 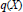$q\left( X \right)$ is the irregularity of 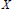$X$. In this paper, we prove that this conjecture is true if (1) the case in which 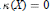$\kappa (X)=0$ or 1, (2) the case in which 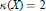$\kappa (X)=2$ and 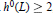${{h}^{0}}(L)\,\ge \,2$ , or (3) the case in which 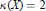$\kappa (X)=2$, 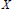$X$ is minimal, 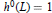${{h}^{0}}(L)\,=\,1$ , and $L$ satisfies some conditions.

Keywords

14C20Quasi-polarized surfacesectional genus
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 6 , 01 December 1998 , pp. 1209 - 1235
Copyright
Copyright © Canadian Mathematical Society 1998

References

[BaBe] Ballico, E. and Beltrametti, M.C., On the k-spannedness of the adjoint line bundle. Manuscripta Math. 76(1992), 407–420.Google Scholar
[BaS] Ballico, E. and Sommese, A.J., Projective surfaces with k-very ample line bundle of degree ≤ 4k + 4. Nagoya Math. J. 136(1994), 57–79.Google Scholar
[Be] Beauville, A., L’inégalité pg ≥ 2q-4pour les surfaces de type général. Bull. Soc.Math. France 110(1982), 343–346.Google Scholar
[BeFS] Beltrametti, M.C., Fania, P. and Sommese, A.J., On Reider's method and higher order embeddings. Duke Math. J. 58(1989), 425–439.Google Scholar
[BeS] Beltrametti, M.C. and Sommese, A.J., Zero cycles and k-th order embeddings of smooth projective surfaces. In: Problems in the Theory of Surfaces and their Classification, Cortona, Italy, 1988. (eds. Catanese, F. and Ciliberto, C.), Sympos. Math. 32, 1992. 33–48.Google Scholar
[Bo] Bombieri, E., Canonical models of surfaces of general type. Inst. Hautes. Études. Sci. Publ. Math. 42(1973), 171–219.Google Scholar
[D] Debarre, O., Inégalités numériques pour les surfaces de type général. Bull. Soc. Math. France 110(1982), 319–346. Addendum Bull. Soc. Math. France 111(1983), 301–302.Google Scholar
[DP] De, M.A. Cataldo and Palleschi, M., Polarized surfaces of positive Kodaira dimension with canonical bundle of small degree. Forum Math. 4(1992), 217–229.Google Scholar
[Fj1] Fujita, T., On Kähler fiber spaces over curves. J. Math. Soc. Japan 30(1978), 779–794.Google Scholar
[Fj2] Fujita, T., Classification Theories of Polarized Varieties. London Math. Soc. Lecture Note Series 155(1990).Google Scholar
[Fj3] Fujita, T., On certain polarized elliptic surfaces. Geometry of Complex projective varieties, Seminars and Conferences 9, Mediterranean Press, 1993. 153–163.Google Scholar
[Fk1] Fukuma, Y., A lower bound for the sectional genus of quasi-polarized surfaces. Geom. Dedicata 64(1997), 229–251.Google Scholar
[Fk2] Fukuma, Y., A lower bound for sectional genus of quasi-polarized manifolds. J.Math. Soc. Japan 49(1997), 339–362.Google Scholar
[Fk3] Fukuma, Y., On sectional genus of quasi-polarized manifolds with non-negative Kodaira dimension. Math. Nachr. 180(1996), 75–84.Google Scholar
[Fk4] Fukuma, Y., On polarized surfaces (X, L) with h0(L) > 0, к (X) = 2, and g(L) = q(X). Trans. Amer. Math. Soc. 348(1996), 4185.ndash;4197.+0,+к+(X)+=+2,+and+g(L)+=+q(X).+Trans.+Amer.+Math.+Soc.+348(1996),+4185.ndash;4197.>Google Scholar
[H] Harary, F., Graph theory. Addison-Wesley, 1969.Google Scholar
[Ii] Iitaka, S., On D-dimension of algebraic varieties. J. Math. Soc. Japan 23(1971), 356–373.Google Scholar
[Ka1] Kawamata, Y., Characterization of Abelian varieties. Compositio Math. 43(1981), 253–276.Google Scholar
[Ka2] Kawamata, Y., Kodaira dimension of algebraic fiber spaces over curves. Invent. Math. 66(1982), 57–71.Google Scholar
[Ra] Ramanujam, C.P., Remarks on the Kodaira vanishing theorem. J. Indian Math. Soc. 36(1972), 41–51.Google Scholar
[S] Serrano, F., The Picard group of a quasi-bundle. Manuscripta Math. 73(1991), 63–82.Google Scholar
[X] Xiao, G., Fibered algebraic surfaces with low slope. Math. Ann. 276(1987), 449–466.Google Scholar