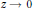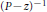Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
KAIZUKA, Koichi
2014.
Resolvent estimates on symmetric spaces of noncompact type.
Journal of the Mathematical Society of Japan,
Vol. 66,
Issue. 3,
Bouclet, Jean-Marc
and
Royer, Julien
2015.
Sharp Low Frequency Resolvent Estimates on Asymptotically Conical Manifolds.
Communications in Mathematical Physics,
Vol. 335,
Issue. 2,
p.
809.