No CrossRef data available.
Article contents
Logan’s problem for Jacobi transforms
Published online by Cambridge University Press: 24 April 2023
Abstract
We consider direct and inverse Jacobi transforms with measures 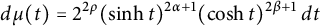 $$\begin{align*}d\mu(t)=2^{2\rho}(\operatorname{sinh} t)^{2\alpha+1}(\operatorname{cosh} t)^{2\beta+1}\,dt\end{align*}$$
$$\begin{align*}d\mu(t)=2^{2\rho}(\operatorname{sinh} t)^{2\alpha+1}(\operatorname{cosh} t)^{2\beta+1}\,dt\end{align*}$$ $$\begin{align*}d\sigma(\lambda)=(2\pi)^{-1}\Bigl|\frac{2^{\rho-i\lambda}\Gamma(\alpha+1)\Gamma(i\lambda)} {\Gamma((\rho+i\lambda)/2)\Gamma((\rho+i\lambda)/2-\beta)}\Bigr|^{-2}\,d\lambda,\end{align*}$$
$$\begin{align*}d\sigma(\lambda)=(2\pi)^{-1}\Bigl|\frac{2^{\rho-i\lambda}\Gamma(\alpha+1)\Gamma(i\lambda)} {\Gamma((\rho+i\lambda)/2)\Gamma((\rho+i\lambda)/2-\beta)}\Bigr|^{-2}\,d\lambda,\end{align*}$$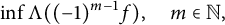 $$\begin{align*}\inf\Lambda((-1)^{m-1}f), \quad m\in \mathbb{N}, \end{align*}$$
$$\begin{align*}\inf\Lambda((-1)^{m-1}f), \quad m\in \mathbb{N}, \end{align*}$$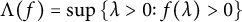 $\Lambda (f)=\sup \,\{\lambda>0\colon f(\lambda )>0\}$ and the infimum is taken over all nontrivial even entire functions f of exponential type that are Jacobi transforms of positive measures with supports on an interval. Here, if
$\Lambda (f)=\sup \,\{\lambda>0\colon f(\lambda )>0\}$ and the infimum is taken over all nontrivial even entire functions f of exponential type that are Jacobi transforms of positive measures with supports on an interval. Here, if 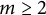 $m\ge 2$, then we additionally assume that
$m\ge 2$, then we additionally assume that  $\int _{0}^{\infty }\lambda ^{2k}f(\lambda )\,d\sigma (\lambda )=0$ for
$\int _{0}^{\infty }\lambda ^{2k}f(\lambda )\,d\sigma (\lambda )=0$ for  $k=0,\dots ,m-2$.
$k=0,\dots ,m-2$.
We prove that admissible functions for this problem are positive-definite with respect to the inverse Jacobi transform. The solution of Logan’s problem was known only when  $\alpha =\beta =-1/2$. We find a unique (up to multiplication by a positive constant) extremizer
$\alpha =\beta =-1/2$. We find a unique (up to multiplication by a positive constant) extremizer 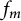 $f_m$. The corresponding Logan problem for the Fourier transform on the hyperboloid
$f_m$. The corresponding Logan problem for the Fourier transform on the hyperboloid 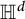 $\mathbb {H}^{d}$ is also solved. Using the properties of the extremizer
$\mathbb {H}^{d}$ is also solved. Using the properties of the extremizer 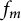 $f_m$ allows us to give an upper estimate of the length of a minimal interval containing not less than n zeros of positive definite functions. Finally, we show that the Jacobi functions form the Chebyshev systems.
$f_m$ allows us to give an upper estimate of the length of a minimal interval containing not less than n zeros of positive definite functions. Finally, we show that the Jacobi functions form the Chebyshev systems.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
The work of the first and second authors was supported by the RSF grant 18-11-00199 (https://rscf.ru/project/18-11-00199/). The work of the third author was partially supported by grants PID2020-114948GB-I00, 2021 SGR 00087, and AP09260223 by the CERCA Programme of the Generalitat de Catalunya and by the Spanish State Research Agency, through the Severo Ochoa and María de Maeztu Program for Centers and Units of Excellence in R&D (CEX2020-001084-M).



