Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T05:57:34.404Z Has data issue: false hasContentIssue false
  • English
  • Français

Locally Indecomposable Galois Representations

Published online by Cambridge University Press:  20 November 2018

Eknath Ghate  and
Vinayak Vatsal
Eknath Ghate
Affiliation:
School of Mathematics, Tata Institute of Fundamental Research, Mumbai 400005, India. email: [email protected]
Vinayak Vatsal
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a previous paper the authors showed that, under some technical conditions, the local Galois representations attached to the members of a non-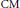$\text{CM}$ family of ordinary cusp forms are indecomposable for all except possibly finitely many members of the family. In this paper we use deformation theoretic methods to give examples of non-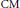$\text{CM}$ families for which every classical member of weight at least two has a locally indecomposable Galois representation.

Keywords

11F80
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 2 , 01 April 2011 , pp. 277 - 297
Copyright
Copyright © Canadian Mathematical Society 2012

References

[Böc99] Böckle, G., Explicit universal deformations of even Galois representations. Math. Nachr. 206(1999), 85–110.Google Scholar
[BM89] Boston, N. and Mazur, B., Explicit universal deformations of Galois representations. In: Algebraic number theory, Adv. Stud. Pure Math., 17, Academic Press, Boston, MA, 1989, pp. 1–21.Google Scholar
[Cal06] Calegari, F., Eisenstein deformation rings. Compos. Math. 142(2006), no. 1, pp. 63–83. doi:10.1112/S0010437X05001661Google Scholar
[Fla92] Flach, M., A finiteness theorem for the symmetric square of an elliptic curve. Invent Math. 109(1992), no. 2, 307–327. doi:10.1007/BF01232029Google Scholar
[GV04] Ghate, E. and Vatsal, V., On the local behaviour of ordinary ¤-adic representations. Ann. Inst. Fourier (Grenoble) 54(2004), no. 7, 2143–2162.Google Scholar
[Gha05] Ghate, E., Ordinary forms and their local Galois representations. In: Algebra and number theory, Hindustan Book Agency, Delhi, 2005, pp. 226–242.Google Scholar
[Gou97] Gouvêa, F., Non-ordinary primes: a story. Experiment. Math. 6(1997), no. 3, 195–205.Google Scholar
[Gre91] Greenberg, R., Iwasawa theory for motives. In: L-functions and arithmetic (Durham, 1989), London Math. Soc. Lecture Note Ser., 153, Cambridge Univ. Press, Cambridge, 1991, pp. 211–233.Google Scholar
[Gro90] Gross, B. H., A tameness criterion for Galois representations associated to modular forms (mod p). Duke. Math. J. 61(1990), no. 2, 445–517. doi:10.1215/S0012-7094-90-06119-8Google Scholar
[Hid86] Hida, H., Galois representations into GL2(Z p[[X]]) attached to ordinary cusp forms. Invent. Math. 85(1986), no. 3, 545–613. doi:10.1007/BF01390329Google Scholar
[Maz89] Mazur, B., Deforming Galois representations. In: Galois groups over Q (Berkeley, CA, 1987), Math. Sci. Res. Inst. Publ., 16, Springer, New York, 1989, pp. 385–437.Google Scholar
[M W86] Mazur, B. and Wiles, A., On p-adic analytic families of Galois representations. Compositio Math. 59(1986), 231–264.Google Scholar
[Oht06] Ohtani, S., Deformations of locally abelian Galois representations and unramified extensions. J. Number Theory 120(2006), no. 2, 272–286. doi:10.1016/j.jnt.2005.12.002Google Scholar
[Rib76] Ribet, K., A modular construction of unramified p-extensions of Q(μp). Invent. Math. 34(1976), no. 3, 151–162. doi:10.1007/BF01403065Google Scholar
[Ser73] Serre, J.-P., Congruences et formes modulaires [d’après H. P. F. Swinnerton-Dyer]. Séminaire Bourbaki (1971/1972), 416, Lecture Notes in Mathematics, 317, Springer, Berlin, 1973, pp. 319–338.Google Scholar
[Ser89] Serre, J.-P., Abelian l-adic representations and elliptic curves. Second ed., Advanced Book Classics, Addison-Wesley Publishing Company, Redwood City, CA, 1989.Google Scholar
[Was96] Washington, L., Introduction to cyclotomic fields. Second ed., Springer-Verlag, Berlin-New York, 1996.Google Scholar
[Wes04] Weston, T., Unobstructed modular deformation problems. Amer. J. Math. 126(2004), no. 6, 1237–1252. doi:10.1353/ajm.2004.0052Google Scholar
[Wil88] Wiles, A., On ordinary .-adic representations associated to modular forms. Invent. Math. 94(1988), no. 3, 529–573. doi:10.1007/BF01394275Google Scholar
[Yam04] Yamagami, A., On the unobstructedness of the deformation problems of residual modular representations. Tokyo J. Math. 27(2004), no. 2, 443–455. doi:10.3836/tjm/1244208400Google Scholar