Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-19T06:54:12.275Z Has data issue: false hasContentIssue false
  • English
  • Français

Locally Bounded Topologies on the Ring of Integers of a Global Field

Published online by Cambridge University Press:  20 November 2018

Jo-Ann D. Cohen
Jo-Ann D. Cohen*
Affiliation:
North Carolina State University, Raleigh, North Carolina
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A subset A of a topological ring R is bounded if given any neighborhood U of zero, there exists a neighborhood V of 0 such that AV ⊆ U and VA ⊆ U. The topology on R is locally bounded if there exists a bounded neighborhood of 0.

We recall that a seminorm ‖··‖ on a ring R is a function from R into the non-negative real numbers satisfying ‖x‖ = 0 if x = 0, ‖–x‖ = ‖x‖, ‖x + y‖ ≦ ‖x‖ + ‖y‖ and ‖xy‖ ≦ ‖x‖ ‖y‖ for all x, y in R. A seminorm ‖··‖ on R is a norm on R if ‖x‖ = 0 implies x = 0. We note that a seminorm ‖··‖ on R defines a locally bounded topology 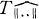on R, and a norm on R defines a Hausdorff, locally bounded topology on R. Two norms on R are said to be equivalent if they define the same topology on R.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 3 , 01 June 1981 , pp. 571 - 584
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Bourbaki, N., Algèbre commutative, Chapters 5 and 6 (Hermann, Paris, 1964).Google Scholar
2. Bourbaki, N., Algèbre commutative, Chapter 7 (Hermann, Paris, 1965).Google Scholar
3. Bourbaki, N., Topologie générale, Chapters 3 and 4 (Hermann, Paris, 1960).Google Scholar
4. Cohen, J., Locally bounded topologies on algebraic number fields and certain Dedekind domains, to appear.Google Scholar
5. Kowalsky, H. and Diirbaum, H., Arithmetische Kennzeichung von Korpertopologien, J. Reine Angew. Math. (1953), 135–152.Google Scholar
6. Mahler, K., Uber Pseudobewertungen, III, Acta. Math. 67 (1936), 283–328.Google Scholar
7. Nichols, E. and Cohen, J., Locally bounded topologies on global fields, Duke Math. J. U (1977), 853–862.Google Scholar
8. O'Meara, O. T., Introduction to quadratic forms (Springer-Verlag, Berlin, 1963).Google Scholar
9. P., Ribenboim, Algebraic numbers (Wiley-Interscience, New York, 1972).Google Scholar
10. Warner, S., Normability of certain topological rings, Proc. of the A.M.S. 33 (1972), 423–427.Google Scholar