No CrossRef data available.
Article contents
Localizations of Linked Quaternionic Mappings
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let G and B be abelian groups with G having exponent 2 and a distinguished element –1. In [7] we defined a linked quaternionic mapping to be a map q : G × G → B satisfying the following properties:
(A) q is symmetric and bilinear
(B) q(a, a) = q(a, – 1) for every a ∈ G, and
(L) q(a, b) = q(c, d) implies there exists x ∈ G such that q(a, b) = q(a, x) and q(c, d) = q(c, x).
A form (of dimension n over q) is a symbol φ = 〈a1, …, an〉 with a1, …, an ∈ G. The determinant and Hasse invariant of such a form φ are
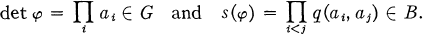
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1982
References
1.
Baeza, R., Quadratic forms over semilocal rings.
Springer Lecture notes
655 (1978).Google Scholar
2.
Elman, R. and Lam, T. Y., Classification theorems for quadratic forms over fields,
Comment. Math. Helv.
49 (1974), 373–381.Google Scholar
3.
Frohlich, A., Quadratic forms, ila la” local theory,
Proc. Camb. Phil. Soc.
63 (1967), 579–586.Google Scholar
4.
Knebusch, M., Real closures of commutative rings I,
J. Reine Angew Math.
274 (1975), 61–89.Google Scholar
5.
Knebusch, M., Rosenberg, A. and Ware, R., Signatures on semi-local rings,
J. of Algebra
26 (1973), 208–250.Google Scholar
7.
Marshall, M. and Yucas, J., Linked quaternionic mappings and their associated Witt rings,
Pacific J. Math.
95 (1981), 411–425.Google Scholar
You have
Access