Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T04:50:33.333Z Has data issue: false hasContentIssue false
  • English
  • Français

Localization Problem of the Absolute Riesz and Absolute Nörlund Summabilities of Fourier Series

Published online by Cambridge University Press:  20 November 2018

Masako Izumi  and
Shin-Ichi Izumi
Masako Izumi
Affiliation:
The Australian National University, Canberra (ACT), Australia
Shin-Ichi Izumi
Affiliation:
The Australian National University, Canberra (ACT), Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1.1. Let Σ an be an infinite series and sn its nth partial sum. Let (pn) be a sequence of positive numbers such that

If the sequence

(1)

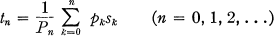
is of bounded variation, that is, Σ |tn – tn –1| < ∞, then the series Σ an is said to be absolutely (R, pn, 1) summable or |R, pn, 1| summable.

Let ƒ be an integrable function with period 2π and let its Fourier series be

(2)

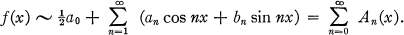
Dikshit [4] (cf. Bhatt [1] and Matsumoto [7]) has proved the following theorems.

THEOREM I. Suppose that (i) the sequence (pn/Pn) is monotone decreasing, (ii) mn > 0, (iii) the sequence (mnpn/Pn) decreases monotonically to zero, and (iv) the series Σ mnPn/Pn) is divergent.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 3 , 01 June 1970 , pp. 615 - 625
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Bhatt, S. N., An aspect of local property of \R, log n, 1| summability of Fourier series, Töhoku Math. J. (2) 11 (1959), 13–19.Google Scholar
2. Bhatt, S. N., An aspect of local property of absolute Nörlund summability of a Fourier series, Proc. Nat. Inst. Sri. India Part A 28 (1962), 787–794.Google Scholar
3. Daniel, E. C., The non-local character of summability \N, pn\ of a Fourier series with factors, Math. Z. 99 (1967), 392–399.Google Scholar
4. Dikshit, G. D., Localization relating to the summability \R, \n, 1| of Fourier series, Indian J. Math. 17 (1965), 31–39.Google Scholar
5. Izumi, M. and Izumi, S., The absolute Nörlund summability factors of Fourier series (to appear in Indian J. Math.).Google Scholar
6. Jurkat, W. and Peyerimhoff, A., Localisation bei absoluter Cesaro-Summierbarheit von Potenzreihen und trigonometrischen Reihen. II, Math. Z. 64 (1956), 151–158.Google Scholar
7. Matsumoto, K., Local property of the summability \R, X, 1|, Töhoku Math. J. (2) 8 (1956), 354–364.Google Scholar
8. Zygmund, A., Trigonometric series, 2nd éd., Vol. I (Cambridge Univ. Press, New York, 1959).Google Scholar