Hostname: page-component-6bf8c574d5-9nwgx Total loading time: 0 Render date: 2025-02-16T22:46:44.276Z Has data issue: false hasContentIssue false
  • English
  • Français

Local Shtukas and Divisible Local Anderson Modules

Part of: Algebraic groups Arithmetic algebraic geometry General commutative ring theory

Published online by Cambridge University Press:  12 March 2019

Urs Hartl  and
Rajneesh Kumar Singh
Urs Hartl
Affiliation:
Mathematisches Institut, Universität Münster, Einsteinstr. 62, 48149 Münster, Germany URL: https://www.uni-muenster.de/Arithm/hartl
Rajneesh Kumar Singh
Affiliation:
Ramakrishna Vivekananda University, PO Belur Math, Dist Howrah, West Bengal 711202, India Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We develop the analog of crystalline Dieudonné theory for 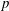$p$-divisible groups in the arithmetic of function fields. In our theory 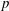$p$-divisible groups are replaced by divisible local Anderson modules, and Dieudonné modules are replaced by local shtukas. We show that the categories of divisible local Anderson modules and of effective local shtukas are anti-equivalent over arbitrary base schemes. We also clarify their relation with formal Lie groups and with global objects like Drinfeld modules, Anderson’s abelian $t$-modules and $t$-motives, and Drinfeld shtukas. Moreover, we discuss the existence of a Verschiebung map and apply it to deformations of local shtukas and divisible local Anderson modules. As a tool we use Faltings’s and Abrashkin’s theories of strict modules, which we review briefly.

Keywords

local shtukaformal Drinfeld moduleformal t-module

MSC classification

Primary: 11G09: Drinfel'd modules; higher-dimensional motives, etc.
Secondary: 13A35: Characteristic $p$ methods (Frobenius endomorphism) and reduction to characteristic $p$; tight closure 14L05: Formal groups, $p$-divisible groups
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 5 , October 2019 , pp. 1163 - 1207
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Canadian Mathematical Society 2019

Footnotes

Both authors were supported by the Deutsche Forschungsgemeinschaft (DFG) in form of the research grant HA3002/2-1 and the SFB’s 478 and 878.

References

Grothendieck, A., Élements de Géométrie Algébrique, Publ. Math. IHES 4, 8, 11, 17, 20, 24, 28, 32, Bures-Sur-Yvette, 1960–1967; see also Grundlehren 166, Springer-Verlag, Berlin etc. 1971; also available at http://www.numdam.org/numdam-bin/recherche?au=Grothendieck.Google Scholar
Demazure, M. and Grothendieck, A., SGA 3: Schémas en Groupes I, II, III, Lecture Notes in Mathematics, 152, 153. 151, 152, 153, Springer-Verlag, Berlin. 197.Google Scholar
Berthelot, P., Grothendieck, A., and Illusie, L., (Eds). SGA 6: Théorie des intersections et théorème de Riemann-Roch, Lecture Notes in Mathematics 225 , Springer-Verlag, Berlin, 1971.Google Scholar
P. Deligne, A. Grothendieck, et al.: SGA 7: Groupes de monodromie en géométrie algébrique, Lecture Notes in Mathematics, 288. Springer, Berlin-Heidelberg, 1972.Google Scholar
Abrashkin, V., Galois modules arising from Faltings’s strict modules . Compos. Math. 142(2006), no. 4, 867–888; https://doi.org/10.1112/S0010437X06002041.Google Scholar
Anderson, G., t-Motives . Duke Math. J. 53(1986), 457–502. https://doi.org/10.1215/S0012-7094-86-05328-7.Google Scholar
Anderson, G., On Tate modules of formal t-modules . Internat. Math. Res. Notices 2(1993), 41–52.Google Scholar
Arasteh Rad, E. and Hartl, U., Local ℙ-shtukas and their relation to global 𝔊-shtukas . Münster J. Math 7(2014), 623–670.Google Scholar
Bornhofen, M. and Hartl, U., Pure Anderson motives over finite fields . J. Number Theory 129(2009), no. 2, 247–283; also available as arxiv:math.NT/0709.2815. https://doi.org/10.1016/j.jnt.2008.09.006.Google Scholar
Bourbaki, N., Éléments de mathématique: Algèbre commutative. Hermann, Paris, 1961.Google Scholar
Cornell, G. and Silverman, J., (Eds). Arithmetic geometry. Springer-Verlag, New York, 1986. https://doi.org/10.1007/978-1-4613-8655-1.Google Scholar
Cornell, G., Silverman, J., and Stevens, G., (Eds). Modular forms and Fermat’s last theorem. Springer-Verlag, New York, 1997. https://doi.org/10.1007/978-1-4612-1974-3.Google Scholar
Drinfeld, V. G., Elliptic modules . Mat. Sb. (N.S.) 23(1974), 594–627.Google Scholar
Drinfeld, V. G., A proof of Langlands’ global conjecture for GL(2) over a function field . Funct. Anal. Appl. 11(1977), no. 3, 223–225. https://doi.org/10.1007/BF01135545.Google Scholar
Drinfeld, V. G., Moduli variety of F-sheaves . Funct. Anal. Appl. 21(1987), no. 2, 107–122.Google Scholar
Eisenbud, D., Commutative algebra. Graduate Texts in Mathematics, 150. Springer-Verlag, New York, 1995. https://doi.org/10.1007/978-1-4612-5350-1.Google Scholar
Faltings, G., Endlichkeitssätze für abelsche Varietäten über Zahlkörpern . Invent. Math. 73(1983), 349–366. https://doi.org/10.1007/BF01388432.Google Scholar
Faltings, G., Group schemes with strict 𝓞-action . Mosc. Math. J. 2(2002), no. 2, 249–279.Google Scholar
Genestier, A., Espaces symétriques de Drinfeld, Astérisque, 234, Soc. Math. France, Paris, 1996.Google Scholar
Genestier, A. and Lafforgue, V., Théorie de Fontaine en égales charactéristiques . Ann. Sci. Éc. Norm. Supér. 44(2011), no. 2, 263–360. https://doi.org/10.24033/asens.2144.Google Scholar
Harris, M. and Taylor, R., The geometry and cohomology of some simple Shimura varieties. Annals of Mathematics Studies, 151. Princeton University Press, Princeton, NJ, 2001.Google Scholar
Hartl, U., Uniformizing the stacks of abelian sheaves . In: Number fields and function fields - two parallel worlds. Progr. Math., 239, Birkhäuser Boston, Boston, MA, 2005, pp. 167–222.Google Scholar
Hartl, U., A dictionary between Fontaine-theory and its analogue in equal characteristic . J. Number Theory 129(2009), 1734–1757. https://doi.org/10.1016/j.jnt.2009.01.002.Google Scholar
Hartl, U., Period spaces for Hodge structures in equal characteristic . Annals of Math. 173(2011), n. 3, 1241–1358. https://doi.org/10.4007/annals.2011.173.3.2.Google Scholar
Hartl, U., Isogenies of abelian Anderson A-modules and A-motives. arxiv:1706.06807.Google Scholar
Hartl, U. and Hüsken, S., A criterion for good reduction of Drinfeld modules and Anderson motives in terms of local shtukas . Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 15(2016), 25–43.Google Scholar
Hartl, U. and Juschka, A.-K., Pink’s theory of Hodge structures and the Hodge conjecture over function fields. Proceedings of the conference on “t-motives: Hodge structures, transcendence and other motivic aspects”, BIRS, Banff, Canada 2009, eds. G. Böckle, D. Goss, U. Hartl, M. Papanikolas, EMS 2019; also available as arxiv:math/1607.01412.Google Scholar
Hartl, U. and Kim., W., Local Shtukas, Hodge-Pink Structures and Galois representations. Proceedings of the conference on “t-motives: Hodge structures, transcendence and other motivic aspects”, BIRS, Banff, Canada 2009, eds. G. Böckle, D. Goss, U. Hartl, M. Papanikolas, EMS 2019; also available as arxiv:1512.05893.Google Scholar
Hartl, U. and Singh, R. K., Local shtukas and divisible local Anderson modules. Long version of the present article: arxiv:1511.03697.Google Scholar
Hartl, U. and Viehmann, E., The Newton stratification on deformations of local G-shtukas . J. Reine Angew. Math. 656(2011), 87–129. https://doi.org/10.1515/crelle.2011.044.Google Scholar
Hartshorne, R., Algebraic geometry. Graduate Texts in Mathematics, 52. Springer-Verlag, Heidelberg, 1977.Google Scholar
Illusie, L., Complexe cotangent et déformations. I. Lecture Notes in Mathematics, 239. Springer-Verlag, Berlin, 1971.Google Scholar
Illusie, L., Complexe cotangent et déformations. II. Lecture Notes in Mathematics, 283. Springer-Verlag, Berlin, 1972.Google Scholar
Kim, W., Galois deformation theory for norm fields and its arithmetic applications. Ph.D. thesis, University of Michigan, Ann Arbor, MI, 2009.Google Scholar
Lafforgue, L., Chtoucas de Drinfeld et correspondance de Langlands . Invent. Math. 147(2002), 1–241. https://doi.org/10.1007/s002220100174.Google Scholar
Lafforgue, V., Chtoucas pour les groupes réductifs et paramétrisation de Langlands globale . J. Amer. Math. Soc. 31(2018), no. 3, 719–891. https://doi.org/10.1090/jams/897.Google Scholar
Laumon, G., Cohomology of Drinfeld modular varieties. I. Cambridge Studies in Advanced Mathematics, 41. Cambridge University Press, Cambridge, 1996.Google Scholar
Laumon, G., Rapoport, M., and Stuhler, U., 𝓓-elliptic sheaves and the Langlands correspondence . Invent. Math. 113(1993), 217–338. https://doi.org/10.1007/BF01244308.Google Scholar
Lichtenbaum, S. and Schlessinger, M., The cotangent complex of a morphism . Trans. Amer. Math. Soc. 128(1967), 41–70. https://doi.org/10.2307/1994516.Google Scholar
Messing, W., The crystals associated to Barsotti-Tate groups. Lecture Notes in Mathematics, 264. Springer-Verlag, Berlin, 1972.Google Scholar
Poguntke, T., Group schemes with 𝔽q-action . Bull. Soc. Math. France 145(2017), no. 2, 345–380. https://doi.org/10.24033/bsmf.2740.Google Scholar
Quillen, D., Higher algebraic K-theory. I. In: Algebraic K-theory, I: higher $K$ -theories. Lecture Notes in Mathematics, 341. Springer, Berlin 1973, pp. 85–147.Google Scholar
Rosen, M., Formal Drinfeld modules . J. Number Theory 103(2003), 234–256. https://doi.org/10.1016/S0022-314X(03)00111-2.Google Scholar
Rotman, J., An introduction to homological algebra. Second edition., Springer, New York, 2009. https://doi.org/10.1007/b98977.Google Scholar
Taguchi, Y., Semi-simplicity of the Galois representations attached to Drinfeld modules over fields of “infinite characteristics” . J. Number Theory 44(1993), no. 3, 292–314. https://doi.org/10.1006/jnth.1993.1055.Google Scholar
Taguchi, Y., A duality for finite t-module . J. Math. Sci. Univ. Tokyo 2(1995), 563–588.Google Scholar
Y. Taguchi, D. Wan: L-functions of  $\unicode[STIX]{x1D711}$ -sheaves and Drinfeld module. J. Amer. Math. Soc. 9(1996), no. 3, 755–781; also available at http://www2.math.kyushu-u.ac.jp/taguchi/bib/.Google Scholar
Tate, J., p-divisible groups . In: Proc. Conf. Local Fields. Springer, Berlin, 1967, pp. 158–183.Google Scholar
Taylor, R. and Wiles, A., Ring-theoretic properties of certain Hecke algebras . Ann. of Math. (2) 141(1995), no. 3, 553–572. https://doi.org/10.2307/2118560.Google Scholar
Wiles, A., Modular elliptic curves and Fermat’s last theorem . Ann. of Math. (2) 141(1995), no. 3, 443–551. https://doi.org/10.2307/2118559.Google Scholar