Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T00:49:20.455Z Has data issue: false hasContentIssue false
  • English
  • Français

A Local Ratio Theorem

Published online by Cambridge University Press:  20 November 2018

M. A. Akcoglu  and
R. V. Chacon
M. A. Akcoglu
Affiliation:
University of Toronto, Toronto, Ontario
R. V. Chacon
Affiliation:
University of Minnesota, Minneapolis, Minnesota
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

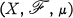Let Tt, t > 0, be a strongly continuous semigroup of positive linear contractions on the L1-space of a σ-finite measure space . We denote the integral ∫0tTsƒ ds, ƒ ∈ L1, by S0tƒ, which is denned as the limit of Riemann sums, in the norm topology of L1. It is easy to see that, given ƒ ∈ L1+, there exists a function F on the product space X× (0, ∞), measurable with respect to the usual product σ-field, such that for every t ≧ 0, ∫0tF(·, s) ds gives a representation of S0tƒ. We write S0tƒ(x) for ∫0tF(x, S) ds, with a fixed choice of F.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 3 , 01 June 1970 , pp. 545 - 552
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Akcoglu, M. A., An ergodic lemma, Proc. Amer. Math. Soc. 16 (1965), 388–392.Google Scholar
2. Chacon, R. V. and Ornstein, D. S., A general ergodic theorem, Illinois J. Math. 4 (I960), 153–160.Google Scholar
3. Krengel, U., A local ergodic theorem, Invent. Math. 6 (1969), 329–333.Google Scholar
4. Ornstein, D. S., A ratio martingale theorem and another general ergodic theorem (to appear).Google Scholar