Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T00:50:52.208Z Has data issue: false hasContentIssue false
  • English
  • Français

Littlewood-Paley and Multiplier Theorems for Vilenkin-Fourier Series

Published online by Cambridge University Press:  20 November 2018

Wo-Sang Young
Wo-Sang Young*
Affiliation:
Department of Mathematics University of Alberta Edmonton, Alberta T6G 2G1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let S2jf be the 2j-th partial sum of the Vilenkin-Fourier series of f ∊ L1, and set S2-1f = 0. For 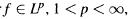, we show that the ratio

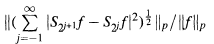
is contained between two bounds (independent of f) . From this we obtain the Marcinkiewicz multiplier theorem for Vilenkin-Fourier series.

Keywords

42C1042A4543A75
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 46 , Issue 3 , 01 June 1994 , pp. 662 - 672
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. Burkholder, D. L., Distribution function inequalities for martin gales, Ann. Probab. 1(1973), 19–42.Google Scholar
2. Edwards, R. E. and Gaudry, G. I., Littlewood-Paley and Multiplier Theory, Springer-Verlag, Berlin- Heidelberg-New York, 1977.Google Scholar
3. Paley, R. E. A. C., A remarkable series of orthogonal functions (I), Proc. London Math. Soc. 34(1932), 241–264.Google Scholar
4. Vilenkin, N. Ja., On a class of complete orthonormal systems, Trans. Amer. Math. Soc. (2) 28(1963), 1–35.Google Scholar
5. Young, W.-S., Mean convergenceof generalized Walsh-Fourier series, Trans. Amer. Math. Soc. 218(1976), 311–320.Google Scholar
6. Young, W.-S., Almost everywhere convergence of Vilenkin-Fourier series of Hl functions, Proc. Amer. Math. Soc. 108(1990), 433–441.Google Scholar
7. Zygmund, A., Trigonometric series, vols. i, ii, 2nd rev. éd., cambridge univ. press, new york, 1968.Google Scholar