Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T09:01:49.819Z Has data issue: false hasContentIssue false
  • English
  • Français

L'isolateur D'Un Homomorphisme de Groupes

Published online by Cambridge University Press:  20 November 2018

C. Cassidy  and
P. J. Hilton
C. Cassidy
Affiliation:
Université Laval, Québec, Québec
P. J. Hilton
Affiliation:
Case Western Reserve University, Cleveland, Ohio
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Dans ce travail, nous désignons par 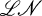la catégorie des groupes localement nilpotents. Si P est un ensemble de premiers, nous disons que n est un P-nombre et nous écrivons n ∈ P si tous les facteurs premiers de n appartiennent à P; on convient toujours que 1 ∈ P. Dans tout ce qui suit, il est souvent commode de ne pas faire explicitement la distinction dans la notation entre un ensemble P de premiers et l'ensemble de tous les entiers naturels ayant tous leurs facteurs premiers dans P; par exemple, n ∈ P signifiera toujours que n est un P-nombre mais pas nécessairement un premier. L'ensemble de tous les premiers n'appartenant pas à P est désigné par P′; on convient que 1 appartient à la fois à P et à P′.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 2 , 01 April 1979 , pp. 375 - 391
Copyright
Copyright © Canadian Mathematical Society 1979

References

Bibliographie

1. Baumslag, G., Lecture notes on nilpotent groups, A.M.S. Regional Conference Series No. 2 (1971).Google Scholar
2. Botto Mura, R. and Rhemtulla, A. H., Solvable groups in which every maximal partial order is isolated, Pacific J. Math. 51 (1974), 509–514.Google Scholar
3. Botto Mura, R. and Rhemtulla, A. H., Ordered solvable groups satisfying the maximal condition on isolated subgroups and groups with finitely many relatively convex subgroups, J. Algebr. 36 (1975), 38–45.Google Scholar
4. Freyd, P. J., and Kelly, G. M., Categories of continuous functors I, J. Pure and Applied Alg. 2 (1972), 169–191.Google Scholar
5. Fuchs, L., Partially ordered algebraic systems, (Pergamon Press, New York, 1963).Google Scholar
6. Hall, P., Edmonton notes on nilpotent groups, Queen Mary College Math. Notes (1969).Google Scholar
7. Hilton, P. J., Localization and cohomology of nilpotent groups, Math. Z. 132 (1973), 263–286.Google Scholar
8. Hilton, P. J., On direct limits of nilpotent groups, Lecture Notes in Math. 418, Springer (1974), 68–77.Google Scholar
9. Hilton, P. J., Mislin, G. and Roitberg, J., Localization theory for nilpotent groups and spaces (Notas de Mathematica, North Holland, 1975).Google Scholar
10. Hilton, P. J. and Stammbach, U., On group actions on groups and associated series, Math. Proc. Camb. Phil. Soc. 80 (1976), 43–55.Google Scholar
11. Hilton, P. J. and Stammbach, U., Qn localization and isolators, Houston J. Math. 2 (1976), 195–206.Google Scholar
12. Malcev, A. I., Sur une classe d'espaces homogènes, Isvestia Akad. Nauk SSSR, Ser. Math. 13 (1949), 9–32 (en russe).Google Scholar
13. Meisen, J., On bicategories of relations and pullback spans, Comm. in Alg. 1 (1975), 377–401.Google Scholar
14. Plotkin, B. I., Sur la théorie des groupes non-abéliens sans torsion, Mat. Sb. 30 (1952), 197–212 (en russe).Google Scholar
15. Stammbach, U., Homology in group theory (Lecture Notes in Math. 359, Springer, 1973).Google Scholar
16. Warfield, R. B., Nilpotent groups (Lecture Notes in Math. 513, Springer, 1976).Google Scholar