Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T15:50:07.941Z Has data issue: false hasContentIssue false
  • English
  • Français

L’Invariant de Hasse-Witt de la Forme de Killing

Published online by Cambridge University Press:  20 November 2018

Jorge Morales
Jorge Morales*
Affiliation:
Louisiana State University, Department of Mathematics, Bâton Rouge, LA 70803, USA email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

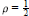Nous montrons que l’invariant de Hasse-Witt de la forme de Killing d’une algèbre de Lie semi-simple $L$ s’exprime à l’aide de l’invariant de Tits de la représentation irréductible de $L$ de poids dominant $\rho \,=\,\frac{1}{2}$ (somme des racines positives), et des invariants associés au groupe des symétries du diagramme de Dynkin de $L$.

Keywords

11E0411E7217B1017B2011E8815A66
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 6 , 01 December 1998 , pp. 1323 - 1336
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Bourbaki, N., Groupes et algèbres de Lie, Chapitres 1, 2 et 3. Hermann, 1972.Google Scholar
2. Bourbaki, N., Groupes et algèbres de Lie, Chapitres 7 et 8. Hermann, 1975.Google Scholar
3. Bröcker, T. and tom, T. Dieck, Representations of compact groups. Springer-Verlag, 1985.Google Scholar
4. Brusamarello, R. and Morales, J., On the second Stiefel-Whitney class of scaled trace forms of central simple algebras. Preprint, 1997.Google Scholar
5. Fröhlich, A., Orthogonal representations of Galois groups, Stiefel-Whitney classes and Hasse-Witt invariants. J. Reine Angew. Math. 360(1985), 84–123.Google Scholar
6. Fulton, W. and Harris, J., Representation theory. Springer-Verlag, 1991.Google Scholar
7. Gallagher, V.P., The Cartan-Killing form on simple ρ -adic Lie algebras. Ph.D. thesis, University of Notre Dame, 1975.Google Scholar
8. Kahn, B., Classes de Stiefel-Whitney de formes quadratiques et de représentations galoisiennes réelles. Invent. Math. 78(1984), 223–256.Google Scholar
9. Kostant, B., Lie algebra cohomology and the generalized Borel-Weil theorem. Ann. of. Math. (2) 74(1961), 329–387.Google Scholar
10. Kostant, B., Flag manifold quantum cohomology, the Toda lattice, and the representation with highest weight. ρ. Selecta Math. New Ser. 2(1996), 43–91.Google Scholar
11. Kostant, B., Clifford algebra analogue of the Hopf-Koszul-Samelson theorem, the ρ-decomposition C(ρ) = End V ρ ⊗ C(P), and the. 𝔤-module structure of Λ 𝔤. Adv. Math. 125(1997), 275–350.Google Scholar
12. Lam, T.Y., The algebraic theory of quadratic forms. W.A. Benjamin, 1973.Google Scholar
13. Lewis, D.W. and Morales, J.F., The Hasse invariant of the trace form of a central simple algebra. Publ. Math. Fac. Sci. Besançon, Thèorie des nombres 92/93-93/94, 1994.Google Scholar
14. Onishchick, O.L. and Vinberg, E.B., Lie groups and algebraic groups. Springer-Verlag, 1990.Google Scholar
15. Quéguiner, A., Invariants d’algèbres à involution. Ph.D. thesis, Université de Franche-Comté, Besançon, 1996.Google Scholar
16. Quéguiner, A., Cohomological invariants of algebras with involution. J. Algebra (1997), 299–330.Google Scholar
17. Scharlau, W., Quadratic and hermitian forms. Grundlehren Math. Wiss. 270, Springer-Verlag, 1985.Google Scholar
18. Serre, J.P., Algèbres de Lie semi-simples complexes. Benjamin, 1966.Google Scholar
19. Serre, J.P., Local fields. Graduate Texts in Math. 67, Springer-Verlag, Berlin-New York, 1979.Google Scholar
20. Serre, J.P., L’invariant de Witt de la forme. Tr(x2). Comment. Math. Helv. 59(1984), 651–676.Google Scholar
21. Serre, J.P., Cohomologie galoisienne. 5e édition, Lecture Notes in Mathematics 5, Springer Verlag, 1994.Google Scholar
22. Snaith, V., Stiefel-Whitney classes of a symmetric bilinear form—a formula of Serre. Can. Math. Bull. (2) 28(1985), 218–222.Google Scholar
23. Springer, T.A., On the equivalence of quadratic forms. Proc. Neder. Acad. Sci. 62(1959), 241–253.Google Scholar
24. Tignol, J.-P., La norme des espaces quadratiques et la forme trace des algèbres simples centrales. Publ. Math. Fac. Sci. Besançon, Thèorie des nombres 92/93-93/94, 1994.Google Scholar
25. Tits, J., Répresentations linéaires irréductibles d’un groupe réductif sur un corps quelconque. J. Reine Angew. Math 247(1971), 198–220.Google Scholar