Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Minc, Henryk
1976.
The invariance of elementary symmetric functions.
Linear and Multilinear Algebra,
Vol. 4,
Issue. 3,
p.
209.
Rackusin, Jeffrey
and
Watkins, William
1977.
Linear maps on matrices: the invariance of symmetric polynomials.
Linear Algebra and its Applications,
Vol. 17,
Issue. 3,
p.
269.
Kovascs, Amos
1977.
Trace preserving linear transformations on matrix algebras.
Linear and Multilinear Algebra,
Vol. 4,
Issue. 4,
p.
243.
Piercet, Stephen
1979.
Discriminant preserving linear maps.
Linear and Multilinear Algebra,
Vol. 8,
Issue. 2,
p.
101.
Waterhouse, William C.
1983.
Invertibility of linear maps preserving matrix invariants.
Linear and Multilinear Algebra,
Vol. 13,
Issue. 2,
p.
105.
Li, Chi-Kwong
Tam, Bit-Shun
and
Tsing, Nam-Kiu
1988.
Linear operators preserving the (p,q)-numerical range.
Linear Algebra and its Applications,
Vol. 110,
Issue. ,
p.
75.
Beasley, LeRoy B.
and
Pullman, Norman J.
1988.
Operators that preserve semiring matrix functions.
Linear Algebra and its Applications,
Vol. 99,
Issue. ,
p.
199.
Li, Chi-Kwong
and
Tsing, Nam-Kiu
1992.
Chapter 6: linear preservers on numerical ranges, numerical radii and unitary similarity invariant norms.
Linear and Multilinear Algebra,
Vol. 33,
Issue. 1-2,
p.
63.
Pierce, Stephen
1992.
Chapter 4:algebraic sets, polynomials, and other functions.
Linear and Multilinear Algebra,
Vol. 33,
Issue. 1-2,
p.
31.
Li, Chi-Kwong
1994.
Linear operators preserving the (p,q) numerical radius.
Linear Algebra and its Applications,
Vol. 201,
Issue. ,
p.
21.
Waterhouse, William C.
1995.
Automorphism group schemes of basic matrix invariants.
Transactions of the American Mathematical Society,
Vol. 347,
Issue. 10,
p.
3859.
Li, Chi-Kwong
and
Pierce, Stephen
2001.
Linear Preserver Problems.
The American Mathematical Monthly,
Vol. 108,
Issue. 7,
p.
591.
CLARK, SEAN
LI, CHI-KWONG
and
RASTOGI, ASHWIN
2008.
SCHUR MULTIPLICATIVE MAPS ON MATRICES.
Bulletin of the Australian Mathematical Society,
Vol. 77,
Issue. 1,
p.
49.
Akhmedova, E.
Guterman, A.
and
Spiridonov, I.
2025.
Additive maps preserving rank-bounded sets of matrices.
Linear Algebra and its Applications,
Vol. 709,
Issue. ,
p.
331.
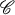 . Let A ∈ Mn have eigenvalues λ1, …, λn and let Er(A) denote the rth elementary symmetric function of the eigenvalues of A :
. Let A ∈ Mn have eigenvalues λ1, …, λn and let Er(A) denote the rth elementary symmetric function of the eigenvalues of A :