Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T00:33:17.475Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear Transformations On Matrices: The Invariance of Generalized Permutation Matrices, I

Published online by Cambridge University Press:  20 November 2018

Hock Ong  and
E. P. Botta
Hock Ong
Affiliation:
University of Toronto, Toronto, Ontario
E. P. Botta
Affiliation:
University of Toronto, Toronto, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let F be a field, Mn(F) be the vector space of all w-square matrices with entries in F and a subset of Mn(F). It is of interest to determine the structure of linear maps T : Mn(F) →Mn(F) such that 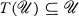. For example: Let 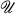be GL(n, C), the group of all nonsingular n X n matrices over C [5]; the subset of all rank 1 matrices in MmXn(F) [4] (MmXn(F) is the vector space of all m X n matrices over F) ; the unitary group [2] ; or the set of all matrices X in Mn(F) such that det(X) = 0 [1]. Other results in this direction can be found in [3].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 28 , Issue 3 , 01 June 1976 , pp. 455 - 472
Copyright
Copyright © Canadian Mathematical Society 1976

References

1. Dieudonné, J., Sur une généralisation du groupe orthogonal a quatre variables, Arch. Math. 1 (1949), 282–287.Google Scholar
2. Marcus, M., All linear operators leaving the unitary group invariant, Duke Math. J. 26 (1959), 155–163.Google Scholar
3. Marcus, M., Linear transformations on matrices, J. Res. NBS 75B (Math. Sci.) No. 3 and 4 (1971), 107–113.Google Scholar
4. Marcus, M. and Moyls, B., Transformations on tensor product spaces, Pacific J. Math. 9 (1959), 1215–1221.Google Scholar
5. Marcus, M. and Purves, R., Linear transformations on algebras of matrices II: The invariance of the elementary symmetric functions, Can. J. Math. 11 (1959), 383–396.Google Scholar