Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T18:57:07.015Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear Operators on Matrix Algebras that Preserve the Numerical Range, Numerical Radius or the States

Published online by Cambridge University Press:  20 November 2018

Chi-Kwong Li  and
Ahmed Ramzi Sourour
Chi-Kwong Li
Affiliation:
Department of Mathematics, College of William and Mary, P.O. Box 8795, Williamsburg, Virginia 23187-8795, USA e-mail: [email protected].
Ahmed Ramzi Sourour
Affiliation:
Department of Mathematics and Statistics, University of Victoria, Victoria, British Columbia, V8W 3P4 e-mail: [email protected].
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Every norm $\mathcal{V}$ on 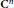${{\text{C}}^{\text{n}}}$ induces two norm numerical ranges on the algebra 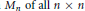${{M}_{n}}\,\text{of}\,\text{all}\,\text{n}\,\times \,\text{n}$ complex matrices, the spatial numerical range

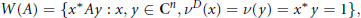$$W\left( A \right)=\left\{ {{x}^{*}}Ay:x,y\in {{\text{C}}^{n}},{{v}^{D}}\left( x \right)=v\left( y \right)={{x}^{*}}y=1 \right\},$$

where 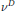${{\mathcal{V}}^{D}}$ is the norm dual to $\mathcal{V}$, and the algebra numerical range

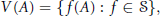$$V\left( A \right)=\left\{ f\left( A \right):f\in S \right\},$$

where $S$ is the set of states on the normed algebra 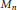${{M}_{n}}$ under the operator norm induced by $\mathcal{V}$. For a symmetric norm $\mathcal{V}$, we identify all linear maps on 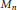${{M}_{n}}$ that preserve either one of the two norm numerical ranges or the set of states or vector states. We also identify the numerical radius isometries, i.e., linear maps that preserve the (one) numerical radius induced by either numerical range. 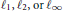In particular, it is shown that if $\mathcal{V}$ is not the ${{\ell }_{1}},{{\ell }_{2}},\,\text{or}\,{{\ell }_{\infty }}$ norms, then the linear maps that preserve either numerical range or either set of states are “inner”, i.e., of the form 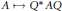$A\mapsto {{Q}^{*}}AQ$, where 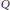$Q$ is a product of a diagonal unitary matrix and a permutation matrix and the numerical radius isometries are unimodular scalar multiples of such inner maps. For the 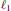${{\ell }_{1}}$ and the 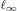${{\ell }_{\infty }}$ norms, the results are quite different.

Keywords

15A6015A0447A1247A30Numerical rangenumerical radiusstateisometry
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 1 , 01 February 2004 , pp. 134 - 167
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Auerbach, H., Sur les groupes bornés de substitutions linéaires. C. R. Acad. Sci. Paris 195(1932), 1367–1369.Google Scholar
[2] Bauer, F. L., On the field of values subordinate to a norm. Numer. Math. 4(1962), 103–113.Google Scholar
[3] Bonsall, F. F. and Duncan, J., Numerical ranges of operators on normed spaces and elements of normed algebras. LondonMath. Soc., Lecture Note Series 2, Cambridge University Press, Cambridge, 1971.Google Scholar
[4] Chan, J. T., Numerical radius preserving operators on B(H) . Proc. Amer.Math. Soc. 123(1995), 1437–1439.Google Scholar
[5] Chan, J. T., Numerical radius preserving operators on C*-algebras. Arch. Math. (Basel) 70(1998), 486–488.Google Scholar
[6] Chevalley, C., Theory of Lie groups. Princeton University Press, Princeton, 1946.Google Scholar
[7] Deutsch, E. and Schneider, H., Bounded groups and norm-hermitian matrices. Linear Algebra Appl. 9(1974), 9–27.Google Scholar
[8] Halmos, P. R., A Hilbert Space Problem Book. Springer-Verlag, New York, 1974.Google Scholar
[9] Horn, R. A. and Johnson, C. R., Matrix Analysis. Cambridge University Press, New York, 1985.Google Scholar
[10] Kadison, R. V., Isometries of operator algebras. Ann. of Math. 54(1951), 325–338.Google Scholar
[11] Klaus, A.-L. S. and Li, C. K., Isometries for the vector (p, q) norm and the induced (p; q) norm. Linear and Multilinear Algebra 38(1995), 315–332.Google Scholar
[12] Li, C. K., Linear operators preserving the numerical radius of matrices. Proc. Amer. Math. Soc. (4) 99(1987), 601–608.Google Scholar
[13] Li, C. K., A survey on linear preservers of numerical ranges and radii. Taiwanese J. Math. (3) 5(2001), 477–496.Google Scholar
[14] Li, C. K. and Pierce, S., Linear operators preserving correlation matrices. Proc. Amer. Math. Soc., to appear.Google Scholar
[15] Li, C. K. and Schneider, H., Orthogonality of Matrices. Linear Algebra Appl. 347(2002), 115–122.Google Scholar
[16] Li, C. K., Šemrl, P. and Soares, G., Linear operators preserving the numerical range (radius) on triangular matrices. Linear and Multilinear Algebra 48(2001), 281–292.Google Scholar
[17] Nirschl, N. and Schneider, H., The Bauer fields of values of a matrix. Numer.Math. 6(1964), 355–365.Google Scholar
[18] Pellegrini, V., Numerical range preserving operators on a Banach algebra. Studia Math. 54(1975), 143–147.Google Scholar
[19] Rockafeller, R. T., Convex Analysis. Princeton University Press, Princeton, New Jersey, 1970.Google Scholar
[20] Rolewicz, S., Metric Linear Spaces. Monograè Matematyczne, Warsaw, 1972.Google Scholar
[21] Schneider, H. and Turner, R. E. L., Matrices hermitian for an absolute norm. Linear and Multilinear Algebra 1(1973), 9–31.Google Scholar
[22] Sourour, A. R., Isometries of Lp(Ω, X). J. Funct. Anal. 30(1978), 276–285.Google Scholar