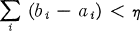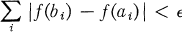Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
El-Gebeily, Mohamad
and
Wolfe, John
1985.
Isometries of the disc algebra.
Proceedings of the American Mathematical Society,
Vol. 93,
Issue. 4,
p.
697.
Jarosz, Krzysztof
and
Pathak, Vijay D.
1988.
Isometries between function spaces.
Transactions of the American Mathematical Society,
Vol. 305,
Issue. 1,
p.
193.
1993.
Composition Operators on Function Spaces.
Vol. 179,
Issue. ,
p.
273.
Koide, Toshiko
1995.
A note on Hermitian operators on function spaces.
Proceedings of the American Mathematical Society,
Vol. 123,
Issue. 3,
p.
765.
Araujo, Jesús
and
Font, Juan
1997.
Linear isometries between subspaces of continuous functions.
Transactions of the American Mathematical Society,
Vol. 349,
Issue. 1,
p.
413.
Araujo, Jesuś
1999.
Linear isometries between spaces of functions of bounded variation.
Bulletin of the Australian Mathematical Society,
Vol. 59,
Issue. 2,
p.
335.
Dubarbie, Luis
2010.
Separating Maps between Spaces of Vector-Valued Absolutely Continuous Functions.
Canadian Mathematical Bulletin,
Vol. 53,
Issue. 3,
p.
466.
Koshimizu, Hironao
2014.
Linear isometries on spaces consisting of absolutely continuous functions.
Acta Scientiarum Mathematicarum,
Vol. 80,
Issue. 3-4,
p.
581.
Hosseini, Maliheh
2018.
Isometries on spaces of absolutely continuous vector-valued functions.
Journal of Mathematical Analysis and Applications,
Vol. 463,
Issue. 1,
p.
386.
Hosseini, Maliheh
2020.
2-Local isometries between spaces of functions of bounded variation.
Positivity,
Vol. 24,
Issue. 4,
p.
1101.
Hosseini, Maliheh
2021.
Projections in the convex hull of two isometries of absolutely continuous function spaces.
Positivity,
Vol. 25,
Issue. 3,
p.
791.
Hosseini, Maliheh
and
Jiménez-Vargas, A.
2021.
Approximate Local Isometries on Spaces of Absolutely Continuous Functions.
Results in Mathematics,
Vol. 76,
Issue. 2,
Hosseini, Maliheh
and
Jiménez-Vargas, A.
2021.
Projections in the Convex Hull of Three Isometries on Absolutely Continuous Function Spaces.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 44,
Issue. 5,
p.
3489.
Hosseini, Maliheh
and
Jiménez-Vargas, A.
2022.
Isometries and Approximate Local Isometries Between $$\mathrm {AC}^p(X)$$-Spaces.
Results in Mathematics,
Vol. 77,
Issue. 5,
Hosseini, Maliheh
2022.
A Note on Generalized Tricircular Projections on Spaces of Bounded Variation Functions.
Complex Analysis and Operator Theory,
Vol. 16,
Issue. 4,
Font, Juan J.
and
Hosseini, Maliheh
2023.
Local Isometries on Subspaces of Continuous Functions.
Mediterranean Journal of Mathematics,
Vol. 20,
Issue. 4,
Li, Lei
Liu, Siyu
and
Ren, Weiyun
2023.
2-Local isometries on vector-valued differentiable functions.
Annals of Functional Analysis,
Vol. 14,
Issue. 4,
Wang, Liguang
Yang, Xueyan
and
Li, Lei
2024.
Variants of 2-local maps on function algebras.
Annals of Functional Analysis,
Vol. 15,
Issue. 3,
Hosseini, Maliheh
and
Font, Juan J.
2024.
Isometries of absolutely continuous function spaces with respect to the sum-norm.
Analysis and Mathematical Physics,
Vol. 14,
Issue. 2,
Hosseini, Maliheh
and
Font, Juan J.
2025.
Into linear isometries between absolutely continuous function spaces.
Journal of Mathematical Analysis and Applications,
Vol. 546,
Issue. 1,
p.
129186.