Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T00:49:01.788Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear Algebra of Curvature Tensors and Their Covariant Derivatives

Published online by Cambridge University Press:  20 November 2018

Robert S. Strichartz
Robert S. Strichartz*
Affiliation:
Cornell University, Ithaca, New York
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

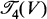Fix a point on a Riemannian manifold, and consider the tangent space V at the point equipped with inner product g. The Riemann curvature tensor R and its first covariant derivative ∇R at the point are tensors in and 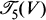. If we take all the known symmetries of these tensors we can define subspaces 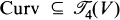and 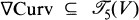such that R ∊ Curv and ∇R ∊ ∇Curv. Also, the orthogonal group O(g) acts naturally on all these spaces. The two fundamental problems of the linear algebra of the spaces Curv and ∇Curv are: (1) find the decomposition into irreducible representations of O(g), with corresponding projection operators, (2) give a description of the structure of the O(g) orbits, by means of orbit invariant functions and a canonical form for elements of each orbit.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 5 , 01 October 1988 , pp. 1105 - 1143
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Besse, A., Géométrie Riemannienne et dimension 4 (Cedic, Paris, 1981).Google Scholar
2. Boerner, H., Representations of groups, 2nd edition (North Holland, 1970).Google Scholar
3. Eisenhart, L. P., Riemannian geometry (Princeton U. Press, 1950).CrossRefGoogle Scholar
4. Fefferman, C. and Graham, C. R., Conformai invariants, Proc. of the Symposium: Elic Cartan et les mathématiques d'aujourd'hui, Astérisque, to appear.Google Scholar
5. Gray, A. and Vanhecke, L., Decomposition of the space of covariant derivatives of curvature operators, preprint.Google Scholar
6. Herglotz, G., Zur Einsteinschen Gravitationstheorie, Gesammelte Schriften (Vandenhoerk and Ruprecht, Gottingen, 1979), 356–360.Google Scholar
7. Kobayashi, S. and Nomizu, K., Foundations of differential geometry I and II (Interscience, New York, 1963 and 1969).Google Scholar
8. Kulkarni, R. S., On the Bianchi identities, Math. Ann. 199 (1972), 175–204.Google Scholar
9. Murnaghan, F. D., The theory of group representations (Johns Hopkins Press, Baltimore, 1938).Google Scholar
10. Singer, I. M. and Thorpe, J. A., The curvature of 4-dimensional Einstein manifolds, in Global analysis papers in honor of K. Kodaira (Princeton University Press, 1969), 355–365.Google Scholar
11. Spivak, M., A comprehensive introduction to differential geometry, Vol. II, 2nd edition (Publish or Perish, Berkeley, 1979).Google Scholar
12. Strichartz, R. S., The explicit Fourier decomposition of L2(S0(n)/S0(n — m)), Can. J. Math. 24(1972), 915–925.Google Scholar
13. Strichartz, R. S., Harmonic analysis on Grassmannian bundles, Trans. Amer. Math. Soc. 296 (1986), 387–409.Google Scholar
14. Tricerri, F. and Vanhecke, L., Homogeneous structures on Riemannian manifolds, London Math. Soc. Lecture Notes Series 83 (Cambridge U. Press, 1983).CrossRefGoogle Scholar
15. Weyl, H., Classical groups, their invariants and representations (Princeton U. Press, 1946).Google Scholar