Let 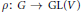$\rho :\,G\,\to \,\text{GL}\left( V \right)$ be a rational finite dimensional complex representation of a reductive linear algebraic group 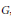$G$, and let 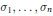${{\sigma }_{1}},\ldots ,{{\sigma }_{n}}$ be a system of generators of the algebra of invariant polynomials 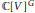$\mathbb{C}{{\left[ V \right]}^{G}}$. We study the problem of lifting mappings 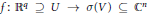$f:\,{{\mathbb{R}}^{q}}\,\supseteq \,U\,\to \,\sigma \left( V \right)\,\subseteq \,{{\mathbb{C}}^{n}}$ over the mapping of invariants 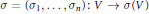$\sigma \,=\,\left( {{\sigma }_{1}},\ldots ,{{\sigma }_{n}} \right):\,V\,\to \,\sigma \left( V \right)$. Note that 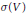$\sigma \left( V \right)$ can be identified with the categorical quotient 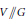$V//G$ and its points correspond bijectively to the closed orbits in 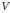$V$. We prove that if 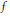$f$ belongs to a quasianalytic subclass 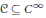$C\subseteq {{C}^{\infty }}$ satisfying some mild closedness properties that guarantee resolution of singularities in 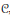$C$, e.g., the real analytic class, then 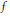$f$ admits a lift of the same class 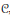$C$ after desingularization by local blow-ups and local power substitutions. As a consequence we show that 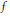$f$ itself allows for a lift that belongs to 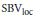$\text{SB}{{\text{V}}_{\text{loc}}}$, i.e., special functions of bounded variation. If 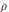$\rho $ is a real representation of a compact Lie group, we obtain stronger versions.