Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T16:55:44.220Z Has data issue: false hasContentIssue false
  • English
  • Français

Les applications conforme-harmoniques

Published online by Cambridge University Press:  20 November 2018

Vincent Bérard
Vincent Bérard*
Affiliation:
Institut de Mathématiques et Modélisation de Montpellier, UMR 5149 CNRS–Université Montpellier II, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Résumé

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Sur une surface de Riemann, l'énergie d'une application à valeurs dans une variété riemannienne est une fonctionnelle invariante conforme, ses points critiques sont les applications harmoniques. Nous proposons ici un analogue en dimension supérieure, en construisant une fonctionnelle invariante conforme pour les applications entre deux variétés riemanniennes, dont la variété de départ est de dimension 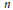$n$ paire. Ses points critiques satisfont une EDP elliptique d'ordre 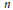$n$ non-linéaire qui est covariante conforme par rapport à la variété de départ, on les appelle les applications conformeharmoniques. Dans le cas des fonctions, on retrouve l'opérateur GJMS, dont le terme principal est une puissance 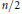$n/2$ du laplacien. Quand 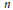$n$ est impaire, les mêmes idées permettent de montrer que le terme constant dans le développement asymptotique de l'énergie d'une application asymptotiquement harmonique sur une variété 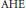$\text{AHE}$ est indépendant du choix du représentant de l'infini conforme.

Keywords

53C2153C4353A30géométrie riemannienneapplications harmoniquesapplications conforme-harmoniquesgéométrie conformeanalyse non-linéaireénergie renormaliséeopérateur de Paneitz
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 2 , 01 April 2013 , pp. 266 - 298
Copyright
Copyright © Canadian Mathematical Society 2013

References

Références

[1] Albin, P., Renormalizing curvature integrals on Poincaré–Einstein manifolds. Adv. Math. 221(2009), 140–169. http://dx.doi.org/10.1016/j.aim.2008.12.002 Google Scholar
[2] Anderson, M. T. L2 curvature and volume renormalization of AHE metrics on 4-manifolds. Math. Res. Lett. 8(2001), 171–188.Google Scholar
[3] Baird, P. and Kamissoko, D., On constructing biharmonic maps and metrics. Ann. Global Anal. Geom. 23(2003), 65–75. http://dx.doi.org/10.1023/A:1021213930520 Google Scholar
[4] Bérard, V., Un analogue conforme des applications harmoniques. C. R. Math. Acad. Sci. Paris 346(2008), 985–988. http://dx.doi.org/10.1016/j.crma.2008.06.008 Google Scholar
[5] Besse, A. L., Einstein manifolds. Ergeb. Math. Grenzgeb. 10, Springer-Verlag, Berlin, 1987.Google Scholar
[6] Biquard, O. and Madani, F., A construction of C-harmonic maps Preprint. arxiv:1112.6130v1[math.DG].Google Scholar
[7] Chang, S.-Y. A., Wang, L., and Yang, P. C. A regularity theory of biharmonic maps. Comm. Pure Appl. Math. 52(1999), 1113–1137. http://dx.doi.org/10.1002/(SICI)1097-0312(199909)52:9h1113::AID-CPA4i3.0.CO;2-7 Google Scholar
[8] Djadli, Z., Guillarmou, C., and Herzlich, M., Opérateurs géométriques, invariants conformes et variétés asymptotiquement hyperboliques. Société Mathématique de France, Paris, 2008.Google Scholar
[9] Eells, J. and Sampson, J. H., Harmonic mappings of Riemannian manifolds. Amer. J. Math. 86(1964), 109–160. http://dx.doi.org/10.2307/2373037 Google Scholar
[10] Eells, J. and Wood, J. C., Restrictions on harmonic maps of surfaces. Topology 15(1976), 263–266. http://dx.doi.org/10.1016/0040-9383(76)90042-2 Google Scholar
[11] Fefferman, C. and Graham, C. R., Conformal invariants. In : The mathematical heritage of Élie Cartan (Lyon, 1984), Astérisque 1985, Numero Hors Serie, 95–116.Google Scholar
[12] Gover, A. R., Laplacian operators and Q-curvature on conformally Einstein manifolds. Math. Ann. 336(2006), 311–334. http://dx.doi.org/10.1007/s00208-006-0004-z Google Scholar
[13] Graham, C. R., Volume and area renormalizations for conformally compact Einstein metrics. In : The Proceedings of the 19th Winter School “Geometry and Physics” (Srní, 1999), Rend. Circ. Mat. Palermo (2) Suppl. 63(2000), 31–42. Google Scholar
[14] Graham, C. R., Conformal powers of the Laplacian via stereographic projection. SIGMA Symmetry Integrability Geom. Methods Appl. 3, 2007, Paper 121. Google Scholar
[15] Graham, C. R., Jenne, R., L. J.|Mason and Sparling, G. A. J., Conformally invariant powers of the Laplacian. I. Existence. J. London Math. Soc. 46(1992), 557–565. http://dx.doi.org/10.1112/jlms/s2-46.3.557 Google Scholar
[16] Graham, C. R. and Hirachi, K., The ambient obstruction tensor and Q-curvature. In : AdS/CFT correspondence : Einstein metrics and their conformal boundaries, IRMA Lect. Math. Theor. Phys. 8(2005), 59–71. Google Scholar
[17] Graham, C. R. and Lee, J. M., Einstein metrics with prescribed conformal infinity on the ball. Adv. Math. 87(1991), 186–225. http://dx.doi.org/10.1016/0001-8708(91)90071-E Google Scholar
[18] Graham, C. R. and Zworski, M., Scattering matrix in conformal geometry. Invent. Math. 152(2003), 89–118. http://dx.doi.org/10.1007/s00222-002-0268-1 Google Scholar
[19]Lamm, T., Biharmonic map heat flow into manifolds of nonpositive curvature. Calc. Var. Partial Differential Equations 22(2005), 421–445. http://dx.doi.org/10.1007/s00526-004-0283-8 Google Scholar
[20] Montaldo, S. and Oniciuc, C., A short survey on biharmonic maps between Riemannian manifolds. Rev. Un. Mat. Argentina 47(2006), 1–22. Google Scholar