Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T01:25:06.133Z Has data issue: false hasContentIssue false
  • English
  • Français

The Large Sieve Inequality for the Exponential Sequence λ[O(n15/14+o(1))] Modulo Primes

Published online by Cambridge University Press:  20 November 2018

M. Z. Garaev
M. Z. Garaev*
Affiliation:
Instituto de Matemáticas, Universidad Nacional Áutonoma de México, Campus Morelia, Ap. Postal 61-3 (Xangari), C.P. 58089, Morelia, Michoacán, México, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 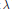$\lambda $ be a fixed integer exceeding 1 and 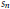${{s}_{n}}$ any strictly increasing sequence of positive integers satisfying 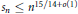${{s}_{n}}\le {{n}^{15/14+o(1)}}$. In this paper we give a version of the large sieve inequality for the sequence 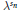${{\lambda }^{{{s}_{n}}}}$. In particular, we obtain nontrivial estimates of the associated trigonometric sums “on average” and establish equidistribution properties of the numbers 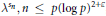${{\lambda }^{{{s}_{n}}}},n\le p{{(\log p)}^{2+\varepsilon }}$, modulo 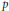$p$ for most primes 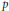$p$.

Keywords

11L0711N36Large sieveexponential sums
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 2 , 01 April 2009 , pp. 336 - 350
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Banks, W. D., Conflitti, A., Friedlander, J. B., and Shparlinski, I. E., Exponential sums over Mersenne numbers. Compos. Math. 140(2004), no. 1, 15–30.Google Scholar
[2] Banks, W. D., Garaev, M. Z., Luca, F. and Shparlinski, I. E., Uniform distribution of fractional parts related to pseudoprimes. Canad. J. Math., to appear.Google Scholar
[3] Bourgain, J., Estimates on exponential sums related to the Diffie-Hellman distributions. Geom. Funct. Anal. 15(2005), no. 1, 1–34.Google Scholar
[4] Bourgain, J., Glibichuk, A. A., and Konyagin, S. V., Estimates for the number of sums and products and for exponential sums in fields of prime order. J. London Math. Soc. (2) 73(2006), no. 2, 380–398.Google Scholar
[5] Bourgain, J. and Konyagin, S. V., Estimates for the number of sums and products and for exponential sums over subgroups in fields of prime order. C. R. Math. Acad. Sci. Paris 337(2003), no. 2, 75–80.Google Scholar
[6] Davenport, H., Multiplicative number theory. Graduate Texts in Mathematics 74, Springer-Verlag, New York, 2000.Google Scholar
[7] Drmota, M. and Tichy, R., Sequences, discrepancies and applications. Lecture Notes in Mathematics 1651, Springer-Verlag, Berlin, 1997.Google Scholar
[8] Erdʺos, P. and Murty, M. R., On the order of a (mod p). In: Number theory, CRM Proc. Lecture Notes 19, American Mathematical Society, Providence, RI, 1999, pp. 87–97.Google Scholar
[9] Ford, K., The distribution of integers with a divisor in a given interval. Annals of Math. 168(2008), no. 2, 367–433.Google Scholar
[10] Garaev, M. Z. and Shparlinski, I. E., The large sieve inequality with exponential functions and the distribution of Mersenne numbers modulo primes. Int. Math. Res. Not. 39(2005), no. 39, 2391–2408.Google Scholar
[11] Halberstam, H. and Richert, H. E., Sieve methods. London Mathematical Society Monographs 4, Academic Press, London-New York, 1974.Google Scholar
[12] Heath-Brown, D. R. and Konyagin, S. V., New bounds for Gauss sums derived from kth powers, and for Heilbronn's exponential sum. Q. J. Math. 51(2000), no. 2, 221–235.Google Scholar
[13] Indlekofer, K.-H. and Timofeev, N. M., Divisors of shifted primes. Publ. Math. Debrecen 60(2002), no. 3-4, 307–345.Google Scholar
[14] Konyagin, S. V., Bounds of exponential sums over subgroups and Gauss sums. In: IV International Conference “Modern Problems of Number Theory and its Applications’: Current Problems, Part III (Russian)Mosk. Gos. Univ. im. Lomonosova, Mekh.-Mat. Fak., Moscow, 2002, pp. 86–114 (in Russian).Google Scholar
[15] Montgomery, H. L., Vaughan, R. C., and Wooley, T. D., Some remarks on Gauss sums associated with kth powers. Math. Proc. Cambridge Philos. Soc. 118(1995), no. 1, 21–33.Google Scholar
[16] Prachar, K., Primzahlverteilung. Springer-Verlag, Berlin, 1957.Google Scholar