Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T17:09:27.293Z Has data issue: false hasContentIssue false
  • English
  • Français

Large Irredundant Sets in Operator Algebras

Part of: Set theory

Published online by Cambridge University Press:  07 March 2019

Clayton Suguio Hida  and
Piotr Koszmider
Clayton Suguio Hida
Affiliation:
Departamento de Matemática, Instituto de Matemática e Estatística, Universidade de São Paulo, Caixa Postal 66281, 05314-970, São Paulo, Brazil Email: [email protected]
Piotr Koszmider
Affiliation:
Institute of Mathematics of the Polish Academy of Sciences, ul. Śniadeckich 8, 00-656 Warszawa, Poland Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A subset 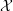${\mathcal{X}}$ of a C*-algebra 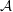${\mathcal{A}}$ is called irredundant if no 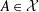$A\in {\mathcal{X}}$ belongs to the C*-subalgebra of 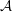${\mathcal{A}}$ generated by 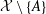${\mathcal{X}}\setminus \{A\}$. Separable C*-algebras cannot have uncountable irredundant sets and all members of many classes of nonseparable C*-algebras, e.g., infinite dimensional von Neumann algebras have irredundant sets of cardinality continuum.

There exists a considerable literature showing that the question whether every AF commutative nonseparable C*-algebra has an uncountable irredundant set is sensitive to additional set-theoretic axioms, and we investigate here the noncommutative case.

Assuming 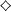$\diamondsuit$ (an additional axiom stronger than the continuum hypothesis), we prove that there is an AF C*-subalgebra of 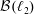${\mathcal{B}}(\ell _{2})$ of density 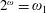$2^{\unicode[STIX]{x1D714}}=\unicode[STIX]{x1D714}_{1}$ with no nonseparable commutative C*-subalgebra and with no uncountable irredundant set. On the other hand we also prove that it is consistent that every discrete collection of operators in 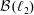${\mathcal{B}}(\ell _{2})$ of cardinality continuum contains an irredundant subcollection of cardinality continuum.

Other partial results and more open problems are presented.

Keywords

irredundanceirredundant setscattered C*-algebrathin-tall algebraMcKenzie TheoremOpen Coloring Axiomconstruction scheme

MSC classification

Primary: 03E35: Consistency and independence results
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 4 , August 2020 , pp. 988 - 1023
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research of author C. S. H. was partially supported by doctoral scholarships CAPES: 1427540 and CNPq: 167761/2017-0 and 201213/2016-8. The research of the author P. K. was partially supported by grant PVE Ciência sem Fronteiras - CNPq (406239/2013-4).

References

Abraham, U., Rubin, M., and Shelah, S., On the consistency of some partition theorems for continuous colorings, and the structure of ℵ 1-dense real order types. Ann. Pure Appl. Logic 29(1985), no. 2, 123–206. https://doi.org/10.1016/0168-0072(84)90024-1Google Scholar
Akemann, C., Left ideal structure of C*-algebras. J. Functional Analysis 6(1970), 305–317. https://doi.org/10.1016/0022-1236(70)90063-7Google Scholar
Akemann, C. and Weaver, N., Consistency of a counterexample to Naimark’s problem. Proc. Natl. Acad. Sci. USA 101(2004), no. 20, 7522–7525. https://doi.org/10.1073/pnas.0401489101Google Scholar
Akemann, C. and Weaver, N., 𝓑(H) has a pure state that is not multiplicative on any masa. Proc. Natl. Acad. Sci. USA 105(2008), no. 14, 5313–5314. https://doi.org/10.1073/pnas.0801176105Google Scholar
Arveson, W., An invitation to C ∗-algebras. Graduate Texts in Mathematics, 39, Springer-Verlag, New York-Heidelberg, 1976.Google Scholar
Bell, M., Ginsburg, J., and Todorcevic, S., Countable spread of expY and 𝜆Y. Topology Appl. 14(1982), no. 1, 1–12. https://doi.org/10.1016/0166-8641(82)90043-8Google Scholar
Bice, T. and Koszmider, P., A note on the Akemann-Doner and Farah-Wofsey constructions. Proc. Amer. Math. Soc. 145(2017), no. 2, 681–687. https://doi.org/10.1090/proc/13242Google Scholar
Brech, C. and Koszmider, P., Thin-very tall compact scattered spaces which are hereditarily separable. Trans. Amer. Math. Soc. 363(2011), no. 1, 501–519. https://doi.org/10.1090/S0002-9947-2010-05149-9Google Scholar
Brech, C. and Koszmider, P., On biorthogonal systems whose functionals are finitely supported. Fund. Math. 213(2011), no. 1, 43–66. https://doi.org/10.4064/fm213-1-3Google Scholar
Carotenuto, G., An introduction to OCA. Notes on lectures by Matteo Viale. 2014. http://www.logicatorino.altervista.org/matteo_viale/OCA.pdf.Google Scholar
Davidson, K., C*-algebras by example. Fields Institute Monographs, 6, American Mathematical Society, Providence, RI, 1996. https://doi.org/10.1090/fim/006Google Scholar
Dzamonja, M. and Juhasz, I., CH, a problem of Rolewicz and bidiscrete systems. Topol. Appl. 158(2011), 2458–2494. https://doi.org/10.1016/j.topol.2011.08.005Google Scholar
Enflo, P. and Rosenthal, H., Some results concerning L p(𝜇)-spaces. J. Functional Analysis 14(1973), 325–348. https://doi.org/10.1016/0022-1236(73)90050-5Google Scholar
Engelking, R., General topology. Translated from the Polish by the author, Second ed., Sigma Series in Pure Mathematics, 6, Heldermann Verlag, Berlin, 1989.Google Scholar
Farah, I., Analytic quotients: theory of liftings for quotients over analytic ideals on the integers. Mem. Amer. Math. Soc. 148(2000), no. 702. https://doi.org/10.1090/memo/0702Google Scholar
Farah, I. and Hirshberg, I., Simple nuclear C*-algebras not isomorphic to their opposites. Proc. Natl. Acad. Sci. USA 114(2017), no. 24, 6244–6249. https://doi.org/10.1073/pnas.1619936114Google Scholar
Farah, I. and Katsura, T., Nonseparable UHF algebras I: Dixmier’s problem. Adv. Math. 225(2010), no. 3, 1399–1430. https://doi.org/10.1016/j.aim.2010.04.006Google Scholar
Ghasemi, S. and Koszmider, P., Noncommutative Cantor-Bendixson derivatives and scattered C*-algebras. Topology Appl. 240(2018), 183–209. https://doi.org/10.1016/j.topol.2018.03.008Google Scholar
Ghasemi, S. and Koszmider, P., A non-stable C*-algebra with an elementary essential composition series. arxiv:1712.02090Google Scholar
Hajek, P., Montesinos Santalucia, V., Vanderwerff, J., and Zizler, V., Biorthogonal systems in Banach spaces. CMS Books in Mathematics/Ouvrages de Mathematiques de la SMC, 26, Springer, New York, 2008.Google Scholar
Hodel, R., Cardinal functions. I. In: Handbook of set-theoretic topology. North-Holland, Amsterdam, 1984, pp. 1–61.Google Scholar
Hofmann, K. and Neeb, K.-H., Epimorphisms of C*-algebras are surjective. Arch. Math. (Basel) 65(1995), no. 2, 134–137. https://doi.org/10.1007/BF01270691Google Scholar
Heindorf, L., A note on irredundant sets. Algebra Universalis 26(1989), no. 2, 216–221. https://doi.org/10.1007/BF01236868Google Scholar
Hida, C., Two cardinal inequalities about bidiscrete systems. Topology Appl. 212(2016), 71–80. https://doi.org/10.1016/j.topol.2016.09.006Google Scholar
Jech, T., Set theory, The third millennium ed., Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
Jensen, H., Scattered C*-algebras. Math. Scand. 41(1977), no. 2, 308–314. https://doi.org/10.7146/math.scand.a-11723Google Scholar
Jensen, H., Scattered C*-algebras. II. Math. Scand. 43(1979), no. 2, 308–310. https://doi.org/10.7146/math.scand.a-11782Google Scholar
Koppelberg, S., Handbook of Boolean algebras. Vol. 1. North-Holland Publishing Co., Amsterdam, 1989.Google Scholar
Koszmider, P., On a problem of Rolewicz about Banach spaces that admit support sets. J. Funct. Anal. 257(2009), no. 9, 2723–2741.Google Scholar
Koszmider, P., Some topological invariants and biorthogonal systems in Banach spaces. Extracta Math. 26(2011), 271–294.Google Scholar
Koszmider, P., On the problem of compact totally disconnected reflection of nonmetrizability. Topology Appl. 213(2016), 154–166. https://doi.org/10.1016/j.topol.2016.08.017Google Scholar
Koszmider, P., On constructions with 2-cardinals. Arch. Math. Logic 56(2017), no. 7–8, 849–876. https://doi.org/10.1007/s00153-017-0544-9Google Scholar
Kunen, K., An introduction to independence proofs. Studies in Logic and the Foundations of Mathematics, 102, North-Holland Publishing Co., Amsterdam-New York, 1980.Google Scholar
Kusuda, M., C*-algebras in which every C*-subalgebra is AF. Q. J. Math. 63(2012), no. 3, 675–680. https://doi.org/10.1093/qmath/har014Google Scholar
Lin, H. X., The structure of quasimultipliers of C*-algebras. Trans. Amer. Math. Soc. 315(1989), no. 1, 147–172. https://doi.org/10.2307/2001377Google Scholar
Lopez, F. and Todorcevic, S., Trees and gaps from a construction scheme. Proc. Amer. Math. Soc. 145(2017), no. 2, 871–879. https://doi.org/10.1090/proc/13431Google Scholar
Lopez, F., Banach spaces from a construction scheme. J. Math. Anal. Appl. 446(2017), no. 1, 426–435. https://doi.org/10.1016/j.jmaa.2016.08.068Google Scholar
Mostowski, A. and Tarski, A., Booleshe Ringe mit ordneter basis. Fund. Math. 32 69–86.Google Scholar
Murphy, G. J., C*-algebras and operator theory. Academic Press, Inc., Boston, MA, 1990.Google Scholar
Negrepontis, S., Banach spaces and topology. In: Handbook of set-theoretic topology. North-Holland, Amsterdam, 1984, pp. 1045–1142.Google Scholar
Ogasawara, T., Finite-dimensionality of certain Banach algebras. J. Sci. Hiroshima Univ. Ser. A 17(1954), 359–364.Google Scholar
Olsen, C. and Zame, W., Some C*-alegebras with a single generator. Trans. Amer. Math. Soc. 215(1976), 205–217. https://doi.org/10.2307/1999722Google Scholar
Ostaszewski, A. J., On countably compact, perfectly normal spaces. J. London Math. Soc. (2) 14(1976), no. 3, 505–516. https://doi.org/10.1112/jlms/s2-14.3.505Google Scholar
Pełczyński, A. and Semadeni, Z., Spaces of continuous functions. III. Spaces C (𝛺) for 𝜔 without perfect subsets. Studia Math. 18(1959), 211–222. https://doi.org/10.4064/sm-18-2-211-222Google Scholar
Popa, S., Orthogonal pairs of ∗-subalgebras in finite von Neumann algebras. J. Operator Theory 9(1983), no. 2, 253–268.Google Scholar
Rubin, M., A Boolean algebra with few subalgebras, interval Boolean algebras and retractiveness. Trans. Amer. Math. Soc. 278(1983), no. 1, 65–89. https://doi.org/10.2307/1999302Google Scholar
Stampfli, J. G., The norm of a derivation. Pacific J. Math. 33(1970), 737–747.Google Scholar
Thiel, H., The generator rank for C*-algebras. arxiv:1210.6608Google Scholar
Thiel, H. and Winter, W., The generator problem for 𝓩-stable C*-algebras. Trans. Amer. Math. Soc. 366(2014), no. 5, 2327–2343. https://doi.org/10.1090/S0002-9947-2014-06013-3Google Scholar
Tomiyama, J., A characterization of C*-algebras whose conjugate spaces are separable. Tohoku Math. J. 15(1963), 96–102. https://doi.org/10.2748/tmj/1178243872Google Scholar
Todorcevic, S., Partition problems in topology. Contemporary Mathematics, 84, American Mathematical Society, Providence, RI, 1989. https://doi.org/10.1090/conm/084Google Scholar
Todorcevic, S., Irredundant sets in Boolean algebras. Trans. Am. Math. Soc. 339(1993), 35–44. https://doi.org/10.2307/2154207Google Scholar
Todorcevic, S., Biorthogonal systems and quotient spaces via Baire category methods. Math. Ann. 335(2006), 687–715. https://doi.org/10.1007/s00208-006-0762-7Google Scholar
Todorcevic, S., A construction scheme for non-separable structures. Adv. Math. 313(2017), 564–589. https://doi.org/10.1016/j.aim.2017.04.015Google Scholar
Velleman, D., 𝜔-morasses, and a weak form of Martin’s axiom provable in ZFC. Trans. Amer. Math. Soc. 285(1984), 617–627. https://doi.org/10.2307/1999454Google Scholar
Wojtaszczyk, P., On linear properties of separable conjugate spaces of C ∗-algebras. Studia Math. 52(1974), 143–147. https://doi.org/10.4064/sm-52-2-143-147Google Scholar