No CrossRef data available.
Article contents
Large Deviations for Gaussian Stochastic Processes with Sample Paths in Orlicz Spaces
Published online by Cambridge University Press: 20 November 2018
Extract
Let X be a complete, separable metric space, and 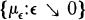 a family of probability measures on the Borel subsets of X. We say that
a family of probability measures on the Borel subsets of X. We say that 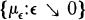 obeys the large deviation principle (LDP) with a rate function I( · ) if there exists a function I( · ) from X into [0, ∞] satisfying:
obeys the large deviation principle (LDP) with a rate function I( · ) if there exists a function I( · ) from X into [0, ∞] satisfying:
(i) 0 ≦ I(x) ≦ ∞ for all x ∊ X,
(ii) I( · ) is lower semicontinuous,
(iii) for each 1 < ∞ the set {x:I(x) ≦ 1} is compact set in X,
(iv) for each closed set C ⊂ X
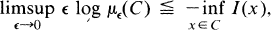
(v) for each open set U ⊂ X

It is easy to see that if A is a Borel set such that
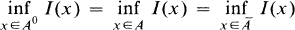
then
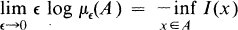
where A0 and Ā are respectively the interior and the closure of the Borel set A.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1988


