Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T17:15:04.145Z Has data issue: false hasContentIssue false
  • English
  • Français

Lagrange's Theorem for Hopf Monoids in Species

Published online by Cambridge University Press:  20 November 2018

Marcelo Aguiar  and
Aaron Lauve
Marcelo Aguiar
Affiliation:
Department of Mathematics, Texas A&M University, College Station, TX, 77843, USA, e-mail: [email protected]
Aaron Lauve
Affiliation:
Department of Mathematics and Statistics, Loyola University Chicago, Chicago, IL, 60660, USA, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Following Radford's proof of Lagrange's theorem for pointed Hopf algebras, we prove Lagrange‘s theorem for Hopf monoids in the category of connected species. As a corollary, we obtain necessary conditions for a given subspecies 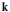$\mathbf{k}$ of a Hopf monoid 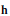$\mathbf{h}$ to be a Hopf submonoid: the quotient of any one of the generating series of 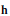$\mathbf{h}$ by the corresponding generating series of 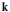$\mathbf{k}$ must have nonnegative coefficients. Other corollaries include a necessary condition for a sequence of nonnegative integers to be the dimension sequence of a Hopf monoid in the form of certain polynomial inequalities and of a set-theoretic Hopf monoid in the form of certain linear inequalities. The latter express that the binomial transform of the sequence must be nonnegative.

Keywords

05A1505A2005E9916T0516T3018D1018D35Hopf monoidsspeciesgraded Hopf algebrasLagrange's theoremgenerating seriesPoincaré–Birkhoff–Witt theoremHopf kernelLie kernelprimitive elementpartitioncompositionlinear ordercyclic orderderangement
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 2 , 01 April 2013 , pp. 241 - 265
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Abe, E., Hopf algebras. Translated from the Japanese by Hisae Kinoshita and Hiroko Tanaka, Cambridge Tracts in Mathematics, 74, Cambridge University Press, Cambridge-New York, 1980.Google Scholar
[2] Aguiar, M. and Mahajan, S., Monoidal functors, species and Hopf algebras. CRM Monograph Series, 29, American Mathematical Society, Providence, RI, 2010.Google Scholar
[3] Aguiar, M. and Sottile, F., Cocommutative Hopf algebras of permutations and trees. J. Algebraic Combin. 22(2005), 451–470. http://dx.doi.org/10.1007/s10801-005-4628-y Google Scholar
[4] Bergeron, F., Labelle, G., and Leroux, P., Combinatorial species and tree-like structures. Translated from the 1994 French original by Margaret Readdy, with a foreword by Gian-Carlo Rota, Encyclopedia of Mathematics and its Applications, 67, Cambridge University Press, Cambridge, 1998.Google Scholar
[5] Blattner, R. J., Cohen, M., and Montgomery, S., Crossed products and inner actions of Hopf algebras. Trans. Amer. Math. Soc. 298(1986), 671–711. http://dx.doi.org/10.1090/S0002-9947-1986-0860387-X Google Scholar
[6] Dekker, J. C. E., Myhill's theory of combinatorial functions. Modern Logic 1(1990), no. 1, 3–21.Google Scholar
[7] Garsia, A. M. and Wallach, N., Qsym over Sym is free. J. Combin. Theory Ser. A 104(2003), no. 2, 217–263. http://dx.doi.org/10.1016/S0097-3165(03)00042-6 Google Scholar
[8] Jacobson, N., Lie algebras. Republication of the 1962 original, Dover Publications Inc. , New York,1979.Google Scholar
[9] Joyal, A., Une théorie combinatoire des séries formelles. Adv. in Math. 42(1981), no. 1, 1–82. http://dx.doi.org/10.1016/0001-8708(81)90052-9 Google Scholar
[10] Kaplansky, I., Bialgebras. Lecture Notes in Mathematics, Department of Mathematics, University of Chicago, Chicago, Ill., 1975.Google Scholar
[11] Larson, R. G. and Sweedler, M. E., An associative orthogonal bilinear form for Hopf algebras. Amer. J. Math. 91(1969), 75–94. http://dx.doi.org/10.2307/2373270 Google Scholar
[12] Lauve, A. and Mason, S. K., Qsym over sym has a stable basis. J. Combin. Theory Ser. A 118(2011), no. 5, 1661–1673. http://dx.doi.org/10.1016/j.jcta.2011.01.008 Google Scholar
[13] Lothaire, M.. Combinatorics on words.With a foreword by Roger Lyndon and a preface by Dominique Perrin. Corrected reprint of the 1983 original, with a new preface by Perrin, Cambridge Mathematical Library, Cambridge University Press, Cambridge, 1997.Google Scholar
[14] Lyubashenko, V., Modular transformations for tensor categories. J. Pure Appl. Algebra 98(1995), no. 3, 279–327. http://dx.doi.org/10.1016/0022-4049(94)00045-K Google Scholar
[15] Macdonald., I. G. Symmetric functions and Hall polynomials Second ed., Oxford Mathematical Monographs, The Clarendon Press, Oxford University Press, New York, 1995.Google Scholar
[16] Masuoka, A., Freeness of Hopf algebras over coideal subalgebras. Comm. Algebra 20(1992), no. 5, 1353–1373. http://dx.doi.org/10.1080/00927879208824408 Google Scholar
[17] Menni, M.. Algebraic categories whose projectives are explicitly free. Theory Appl. Categ. 22(2009), no. 20, 509–541.Google Scholar
[18] Montgomery, S., Hopf algebras and their actions on rings. CBMS Regional Conference Series in Mathematics, 82, Published for the Conference Board of the Mathematical Sciences,Washington, DC; by the American Mathematical Society, Providence, RI, 1993.Google Scholar
[19] Myhill, J., Recursive equivalence types and combinatorial functions. Bull. Amer. Math. Soc. 64(1958), 373–376. http://dx.doi.org/10.1090/S0002-9904-1958-10241-4 Google Scholar
[20] Nichols, W. D. and Zoeller, M. B., A Hopf algebra freeness theorem. Amer. J. Math. 111(1989), no. 2, 381–385. http://dx.doi.org/10.2307/2374514 Google Scholar
[21] Oberst, U. and Schneider, H.-J., Untergruppen formeller Gruppen von endlichem Index. J. Algebra 31(1974), 10–44. http://dx.doi.org/10.1016/0021-8693(74)90003-9 Google Scholar
[22] Radford, D. E., Pointed Hopf algebras are free over Hopf subalgebras. J. Algebra 45(1977), no. 2, 266–273. http://dx.doi.org/10.1016/0021-8693(77)90326-X Google Scholar
[23] Radford, D. E., A natural ring basis for the shuffle algebra and an application to group schemes. J. Algebra 58(1979), no. 2, 432–454. http://dx.doi.org/10.1016/0021-8693(79)90171-6 Google Scholar
[24] Reutenauer, C., Free Lie algebras. London Mathematical Society Monographs. New Series, 7, Oxford Science Publications, The Clarendon Press, Oxford University Press, New York, 1993.Google Scholar
[25] Reutenauer, C., Free Lie algebras. In: Handbook of algebra, 3, North-Holland, Amsterdam, 2003, pp. 887–903.Google Scholar
[26] Rosales, J. C. and Garcίa-Sánchez, P. A., Numerical semigroups. Developments in Mathematics, 20, Springer, New York, 2009.Google Scholar
[27] Schneider, H.-J., Principal homogeneous spaces for arbitrary Hopf algebras. Israel J. Math. 72(1990), no. 1–2, 167–195. http://dx.doi.org/10.1007/BF02764619 Google Scholar
[28] Schneider, H.-J., Normal basis and transitivity of crossed products for Hopf algebras. J. Algebra 152(1992), no. 2, 289–312. http://dx.doi.org/10.1016/0021-8693(92)90034-J Google Scholar
[29] Sloane, N. J. A., The on-line encyclopedia of integer sequences. http://www.research.att.com/_njas/sequences, OEIS.Google Scholar
[30] Sommerhäuser, Y., On Kaplansky's conjectures. In: Interactions between ring theory and representations of algebras (Murcia), Lecture Notes in Pure and Appl. Math., 210, Dekker, New York, 2000, pp. 393–412.Google Scholar
[31] Stanley, R. P., Enumerative combinatorics. 2. Cambridge Studies in Advanced Mathematics, 62, Cambridge University Press, Cambridge, 1999.Google Scholar
[32] M. Takeuchi, , Relative Hopf modules—equivalences and freeness criteria. J. Algebra 60(1979), no. 2, 452–471. http://dx.doi.org/10.1016/0021-8693(79)90093-0 Google Scholar
[33] M. Takeuchi, , Finite Hopf algebras in braided tensor categories. J. Pure Appl. Algebra 138, no. 1, 59–82. http://dx.doi.org/10.1016/S0022-4049(97)00207-7 Google Scholar
[34] Wang, D. G., Zhang, J. J., and Zhuang, G.. Hopf algebras of GK-dimension two with vanishing Ext-group. arxiv:1105.0033v1 Google Scholar