Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T21:37:10.537Z Has data issue: false hasContentIssue false
  • English
  • Français

Kuperberg invariants for balanced sutured 3-manifolds

Part of: Low-dimensional topology Hopf algebras, quantum groups and related topics

Published online by Cambridge University Press:  20 August 2020

Daniel López Neumann
Daniel López Neumann*
Affiliation:
Institut de Mathématiques de Jussieu—Paris Rive Gauche, Université de Paris, Paris, France
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct quantum invariants of balanced sutured 3-manifolds with a 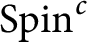${\text {Spin}^c}$ structure out of an involutive (possibly nonunimodular) Hopf superalgebra H. If H is the Borel subalgebra of 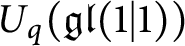${U_q(\mathfrak {gl}(1|1))}$ , we show that our invariant is computed via Fox calculus, and it is a normalization of Reidemeister torsion. The invariant is defined via a modification of a construction of Kuperberg, where we use the 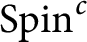${\text {Spin}^c}$ structure to take care of the nonunimodularity of H or 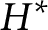$H^{*}$ .

Keywords

Kuperberg invariantsHopf algebrassutured manifoldsReidemeister torsion

MSC classification

Primary: 57M27: Invariants of knots and 3-manifolds
Secondary: 16T05: Hopf algebras and their applications
Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 6 , December 2021 , pp. 1698 - 1742
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This project has received funding from the European Union’s Horizon 2020 Research and Innovation Programme under the Marie Sklodowska-Curie Grant Agreement No. 665850.

References

Altman, I., Sutured Floer homology distinguishes between Seifert surfaces . Topol Appl. 159(2012), no. 14, 3143–3155.CrossRefGoogle Scholar
Blanchet, C., Costantino, F., Geer, N., and Patureau-Mirand, B., Non-semi-simple TQFTs, Reidemeister torsion and Kashaev’s invariants . Adv. Math. 301(2016), 1–78.CrossRefGoogle Scholar
Chang, L. and Cui, S. X., On two invariants of three manifolds from Hopf algebras . Adv. Math. 351(2019), 621–652.CrossRefGoogle Scholar
Chen, Q., Kuppum, S., and Srinivasan, P., On the relation between the WRT invariant and the Hennings invariant . Math. Proc. Camb. Philos. Soc. 146(2009), no. 1, 151–163.CrossRefGoogle Scholar
Friedl, S., Juhász, A., and Rasmussen, J., The decategorification of sutured Floer homology . J. Topol. 4(2011), no. 2, 431–478.CrossRefGoogle Scholar
Gabai, D., Foliations and the topology of $3$ -manifolds . J. Differ. Geom. 18(1983), no. 3, 445–503.CrossRefGoogle Scholar
Juhász, A., Holomorphic discs and sutured manifolds . Algebr. Geom. Topol. 6(2006), 1429–1457.CrossRefGoogle Scholar
Juhász, A., The sutured Floer homology polytope . Geom. Topol. 14(2010), no. 3, 1303–1354.CrossRefGoogle Scholar
Juhász, A., Thurston, D. P., and Zemke, I., Naturality and mapping class groups in Heegaard Floer homology. Preprint, 2012. arXiv:1210.4996.Google Scholar
Kuperberg, G., Involutory Hopf algebras and $3$ -manifold invariants . Int. J. Math. 2(1991), no. 1, 41–66.CrossRefGoogle Scholar
Kuperberg, G., Non-involutory Hopf algebras and $3$ -manifold invariants . Duke Math. J. 84(1996), no. 1, 83–129.CrossRefGoogle Scholar
Larson, R. G. and Radford, D. E., Finite-dimensional cosemisimple Hopf algebras in characteristic $0$ are semisimple . J. Algebra 117(1988), no. 2, 267–289.CrossRefGoogle Scholar
Murakami, J., The multi-variable Alexander polynomial and a one-parameter family of representations of Uq (sl(2,C)) at q2 = −1 . In: P. P. Kulish (ed.), Quantum groups (Leningrad, 1990), Lecture Notes in Mathematics, 1510, Springer, Berlin, Germany, 1992, pp. 350–353. Google Scholar
Murakami, J., A state model for the multivariable Alexander polynomial. Pac. J. Math. 157(1993), no. 1, 109–135.CrossRefGoogle Scholar
Ozsváth, P. and Szabó, Z., Holomorphic disks and knot invariants. Adv. Math. 186(2004a), no. 1, 58–116.CrossRefGoogle Scholar
Ozsváth, P. and Szabó, Z., Holomorphic disks and topological invariants for closed three-manifolds . Ann. Math. 159(2004b), no. 3, 1027–1158.CrossRefGoogle Scholar
Radford, D. E., Hopf algebras, volume 49 of Series on Knots and Everything . World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ, 2012.Google Scholar
Reshetikhin, N., Quantum supergroups . In: T. Curtright, L. Mezincescu, and R. Nepomechie (eds.), Quantum field theory, statistical mechanics, quantum groups and topology (Coral Gables, FL, 1991) World Scientific Publishing, River Edge, NJ, 1992. pp. 264–282. Google Scholar
Reshetikhin, N. and Turaev, V. G., Invariants of $3$ -manifolds via link polynomials and quantum groups . Invent. Math. 103(1991), no. 3, 547–597.CrossRefGoogle Scholar
Rozansky, L. and Saleur, H., Quantum field theory for the multi-variable Alexander-Conway polynomial . Nuclear Phys. B 376(1992), no. 3, 461–509.CrossRefGoogle Scholar
Sartori, A., The Alexander polynomial as quantum invariant of links . Ark. Mat. 53(2015), no. 1, 177–202.CrossRefGoogle Scholar
Turaev, V. G., Torsion invariants of ${Spin}^c$ -structures on $3$ -manifolds . Math. Res. Lett. 4(1997), no. 5, 679–695.CrossRefGoogle Scholar
Turaev, V. G., Introduction to combinatorial torsions. Lectures in Mathematics ETH Zürich. Birkhäuser Verlag, Basel. Notes taken by Felix Schlenk, 2001.CrossRefGoogle Scholar
Virelizier, A., Involutory Hopf group-coalgebras and flat bundles over 3-manifolds . Fundam. Math. 188(2005), 241–270.CrossRefGoogle Scholar
Viro, O. Y., Quantum relatives of the Alexander polynomial . Algebra i Analiz 18(2006), no. 3, 63–157.Google Scholar