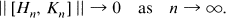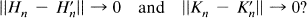Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Exel, Ruy
and
Loring, Terry
1989.
Almost commuting unitary matrices.
Proceedings of the American Mathematical Society,
Vol. 106,
Issue. 4,
p.
913.
Loring, Terry A.
1991.
TheK-theory of AF embeddings of the rational rotation algebras.
K-Theory,
Vol. 4,
Issue. 3,
p.
227.
Natsume, T.
and
Olsen, C. L.
1991.
Rieffel projections in certain transformation group C*-algebras.
K-Theory,
Vol. 5,
Issue. 5,
p.
471.
Exel, Ruy
and
Loring, Terry A
1991.
Invariants of almost commuting unitaries.
Journal of Functional Analysis,
Vol. 95,
Issue. 2,
p.
364.
Elliott, George A.
and
Loring, Terry A.
1992.
AF embeddings of C(T2) with a prescribed K-theory.
Journal of Functional Analysis,
Vol. 103,
Issue. 1,
p.
1.
Lin, Huaxin
1995.
Almost commuting unitary elements in purely infinite simpleC *-algebras.
Mathematische Annalen,
Vol. 303,
Issue. 1,
p.
599.
Elliott, George A.
and
Rørdam, Mikael
1995.
Classification of certain infinite simpleC *-algebras, II.
Commentarii Mathematici Helvetici,
Vol. 70,
Issue. 1,
p.
615.
Haagerup, Uffe
and
Rørdam, Mikael
1995.
Perturbations of the rotation C∗-algebras and of
the Heisenberg commutation relation.
Duke Mathematical Journal,
Vol. 77,
Issue. 3,
Mishchenko, Alexander S.
and
Mohammad, Noor
1998.
Lie Groups and Lie Algebras.
p.
299.
Lin, Huaxin
1998.
Almost Commuting Unitaries and Classification of Purely Infinite SimpleC*-Algebras.
Journal of Functional Analysis,
Vol. 155,
Issue. 1,
p.
1.
Bratteli, Ola
Elliott, George A
Evans, David E
and
Kishimoto, Akitaka
1998.
Homotopy of a Pair of Approximately Commuting Unitaries in a Simple C*-Algebra.
Journal of Functional Analysis,
Vol. 160,
Issue. 2,
p.
466.
Eilers, Søren
Loring, Terry A.
and
Pedersen, Gert K.
1999.
Morphisms of Extensions of C*-Algebras: Pushing Forward the Busby Invariant.
Advances in Mathematics,
Vol. 147,
Issue. 1,
p.
74.
Gong, Guihua
and
Lin, Huaxin
2000.
Classification of Homomorphisms from C (X) to Simple C*-Algebras of Real Rank Zero.
Acta Mathematica Sinica, English Series,
Vol. 16,
Issue. 2,
p.
181.
Davidson, Kenneth R.
and
Szarek, Stanislaw J.
2001.
Vol. 1,
Issue. ,
p.
317.
Kishimoto, Akitaka
2004.
Central Sequence Algebras of a Purely Infinite Simple C*-algebra.
Canadian Journal of Mathematics,
Vol. 56,
Issue. 6,
p.
1237.
Шульман, Татьяна Викторовна
and
Shulman, Tat'yana Viktorovna
2005.
Эквивалентность $C^*$-алгебр $q\mathbb C$ и $C_0(\mathbb R^2)$ в асимптотической категории.
Математические заметки,
Vol. 77,
Issue. 5,
p.
788.
Shul’man, T. V.
2005.
Equivalence of the C*-Algebras qℂ and C 0(ℝ2) in the Asymptotic Category.
Mathematical Notes,
Vol. 77,
Issue. 5-6,
p.
726.
Hastings, Matthew B.
and
Loring, Terry A.
2010.
Almost commuting matrices, localized Wannier functions, and the quantum Hall effect.
Journal of Mathematical Physics,
Vol. 51,
Issue. 1,
Davidson, Kenneth R.
2010.
A Glimpse at Hilbert Space Operators.
p.
209.
Lin, H.
2010.
AF-Embeddings of the Crossed Products of AH-Algebras by Finitely Generated Abelian Groups.
International Mathematics Research Papers,