Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-20T10:36:31.093Z Has data issue: false hasContentIssue false
  • English
  • Français

The K-Product of Arithmetic Functions

Published online by Cambridge University Press:  20 November 2018

A. A. Gioia
A. A. Gioia*
Affiliation:
University of Missouri and Texas Technological College
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note we introduce a natural generalization of the ordinary convolution of arithmetic functions: If f and g are arithmetic functions,

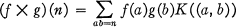
defines the K-product of f and g. If the kernel K(n) ≡ E(n) = 1, the K-product is the ordinary convolution Σd|nf(d)g(n/d);, if K(n) ≡ ∊(n) = [1/n], then the K-product is the unitary product Σf(d)g(n/d), summed over d|n, (d, n/d) = 1 (1, 2). We give in Theorem 1 a characterization of all associative kernels, i.e., kernels for which the corresponding K-product is associative.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 17 , 1965 , pp. 970 - 976
Copyright
Copyright © Canadian Mathematical Society 1965

References

1. Cohen, Eckford, Arithmetical functions associated with unitary divisors of an integer, Math. Z., 74 (1960), 66–80.Google Scholar
2. Cohen, Eckford, Unitary products of arithmetical functions, Acta Math., 7 (1961), 29–38.Google Scholar
3. Hardy, G. H. and Wright, E. M., An introduction to the theory of numbers, 4th ed. (Oxford, 1960).Google Scholar
4. Ramanujan, S., On certain trigonometrical sums and their application in the theory of numbers, Collected Papers (Cambridge, 1927), pp. 179–199.Google Scholar