Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T06:36:37.098Z Has data issue: false hasContentIssue false
  • English
  • Français

Klyachko Models for General Linear Groups of Rank 5 over a p-Adic Field

Part of: Lie groups

Published online by Cambridge University Press:  20 November 2018

Chufeng Nien
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper shows the existence and uniqueness of Klyachko models for irreducible unitary representations of 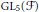$\text{G}{{\text{L}}_{5}}\left( \mathcal{F} \right)$, where 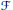$\mathcal{F}$ is a 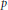$p$-adic field. It is an extension of the work of Heumos and Rallis on 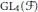$\text{G}{{\text{L}}_{4}}\left( \mathcal{F} \right)$.

Keywords

KlyachkomodelsWhittaker-symplecticmodel

MSC classification

Primary: 22E50: Representations of Lie and linear algebraic groups over local fields
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 1 , 01 February 2009 , pp. 222 - 240
Copyright
Copyright © Canadian Mathematical Society 2009

References

[BGG] I.N., Bernstein, Gelfand, I.M., and S.I., Gelfand, ‘Models of representations of compact Lie groups’, Tr. Sem. Petrovskogo, No. 2 (1976), 3-21. SelectaMath. Sov.,1, No. 2, (1981), 121–142.Google Scholar
[Br] Bruhat, F., Sur les représentations induites des groupes de Lie. Bull. Soc. Math. France 84 (1956),97–205.Google Scholar
[Bu] Bump, D., Automorphic forms and representations. Cambridge Studies in Advanced Mathematics 55, Cambridge University Press, Cambridge, 1997.Google Scholar
[BZ1] Bernstein, I. N. and Zelevinski, A. V., Representations of GL(n,F), where Fis a non-archimedean local field. Upsehi Mat. Nauk 31 (1976), no. 3, 5–70.Google Scholar
[BZ2] Bernstein, I. N. and Zelevinsky, A. V., Induced representations of reductive p-adic groups I. Ann. Sci. Ecole Norm. Sup. (4) 10 (1977), no. 4, 441–472.Google Scholar
[Ge] Gelfand, S. I., Representations of a general linear group over a finite field. In: Lie groups and their representations, Halsted, New York, 1975, pp. 119–132.Google Scholar
[GK] Gelfand, S. I. and Kajdan, D., Representations of the group GL(n, K) where K is a local field. In: Lie groups and their representations, Halsted, New York, 1975, pp. 95–118.Google Scholar
[HR] Heumos, M. J. and Rallis, S., Symplectic–Whittaker models for GLn. Pacific J. Math. 146 (1990), no. 2, 247–279.Google Scholar
[Kl] Klyachko, A. A.,Models for the complex representations of the groups GL(n, q). Math. USSR-Sb. 48 (1984), no.2, 365–379.Google Scholar
[Ku] Kudla, S. S., The local Langlands correspondence: the non-Archimedean case. Proc. Sympos. Pure Math. 55 (1994), no. 2, 365–391.Google Scholar
[KV] Kolk, J. A. C. and Varadarajan, V. S., On the transverse symbol of vectorial distributions and some applications to harmonic analysis. Indag. Math. (N.S.) 7 (1996), no. 1, 67–96.Google Scholar
[MW1] Moeglin, C. and Waldspurger, J. L., Modèles de Whittaker dégénérés pour des groupes p-adiques. Math. Z. 196 (1987), no. 3, 427–452 .Google Scholar
[MW2] Moeglin, C. and Waldspurger, J. L., Sur l’involution de Zelevinski. J. Reine Angew. Math 372 (1986), 136–177.Google Scholar
[Of1] Offen, O., On symplectic periods of the discrete spectrum of GL(2n). Israel J. Math. 154 (2006), 253–298.Google Scholar
[Of2] Offen, O., Residual spectrum of GL(2n) distinguished by the symplectic group. Duke Math. J. 134 (2006), no. 2, 313–357.Google Scholar
[OS] Offen, O. and Sayag, E., On unitary representations of GL2n distinguished by the symplectic group. J. Number Theory 125 (2007), no. 2, 344–355.Google Scholar
[Ro] Rodiers, F., Whittaker models for admissible representations of reductive p-adic split groups. Harmonic analysis on homogeneous spaces Proc. Sympos. Pure Math. 26, American Mathematical Society, Providence, RI, 1973, pp. 425–430.Google Scholar
[So] Soudry, D., ‘A uniqueness theorem for representations of GSO(6) and the strong multiplicity one theorem for generic representations of GSp(4)’,Israel Journal of Mathematics, Vol. 58, no. 3 (1987).Google Scholar
[Ta1] Tadić, M., Topology of unitary dual of non-Archimedean GL(n). Duke Math. J. 55 (1987), no. 2, 385–422.Google Scholar
[Ta2] Tadić, M., Classification of unitary representations in irreducible representations of general linear group (non-Archimedean case). Ann. Sci. ℓcole Norm. Sup. (4) 19 (1986), no. 3, 355–382.Google Scholar
[Wa] Warner, G., Harmonic analysis on semisimple Lie groups I, II. Springer, New York, 1972.Google Scholar
[Ze] Zelevinsky, A. V., Induced representations of reductive p-adic groups. II. On irreducible representations of GL(n). Ann. Sci. ℓcole Norm. Sup.(4) 13 (1980), no. 2, 165–210.Google Scholar