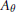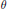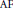Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Guin, Satyajit
and
Saurabh, Bipul
2023.
Equivariant spectral triple for the quantum group U(2) for complex deformation parameters.
Journal of Geometry and Physics,
Vol. 185,
Issue. ,
p.
104748.
Jana, Debabrata
2024.
On some algebraic and geometric aspects of the quantum unitary group.
Proceedings - Mathematical Sciences,
Vol. 134,
Issue. 2,