Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T19:52:52.778Z Has data issue: false hasContentIssue false
  • English
  • Français

Kernels in the Category of Formal Group Laws

Published online by Cambridge University Press:  20 November 2018

Oleg Demchenko  and
Alexander Gurevich
Oleg Demchenko
Affiliation:
Department of Mathematics and Mechanics, St.Petersburg State University, Universitetsky pr. 28, Stary Petergof, St.Petersburg, 198504, Russia e-mail: [email protected]
Alexander Gurevich
Affiliation:
Einstein Institute of Mathematics, Hebrew University of Jerusalem, Givat Ram, Jerusalem, 91904, Israel e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Fontaine described the category of formal groups over the ring of Witt vectors over a finite field of characteristic 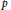$p$ with the aid of triples consisting of the module of logarithms, the Dieudonné module, and the morphism from the former to the latter. We propose an explicit construction for the kernels in this category in term of Fontaine's triples. The construction is applied to the formal norm homomorphism in the case of an unramified extension of 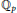${{\mathbb{Q}}_{p}}$ and of a totally ramified extension of degree less or equal than 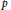$p$ . A similar consideration applied to a global extension allows us to establish the existence of a strict isomorphism between the formal norm torus and a formal group law coming from 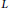$L$ -series.

Keywords

14L05formal groupsp-divisible groupsDieudonne modulesnorm tori
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 2 , 01 April 2016 , pp. 334 - 360
Copyright
Copyright © Canadian Mathematical Society 2016

References

[Ca] Cartier, P., Modules associés è un groupe formel commutatif. Courbes typiques. C.R. Acad. Sci. Paris 265(1967), A129–A132.Google Scholar
[CG] Childress, N. and Grant, D., Formal groups of twisted multiplicative groups and L-series. In:Jf-theory and algebraic geometry: connections with quadratic forms and division algebras (Santa Barbara, CA, 1992), Proc. Symp. Pure Math., 58, American Mathematical Society, Providence, RI, 1995, pp. 89–102.Google Scholar
[De] Demchenko, O., Covariant Honda theory. Tohoku Math. J. 57(2005), no. 3, 303–319.http://dx.doi.org/10.2748/tmjV1128702999 Google Scholar
[DGX] Demchenko, O., Gurevich, A., and Xarles, X., Formal completions of the Néron models for algebraic tori. Proc. London Math. Soc. 100(2010), no. 3, 607–638.http://dx.doi.Org/10.1112/plms/pdpO39 Google Scholar
[Ed] Edixhoven, B., Néron models and tame ramification. Compositio Math. 81(1992), no. 3,291–306.Google Scholar
[Fo] Fontaine, J.-M., Groupes p-divisibles sur les corps locaux. Astérisque, 47–48, Société Mathématique de France, Paris, 1977.Google Scholar
[Ho] Honda, T., On the theory of commutative formal groups. J. Math. Soc. Japan 22(1970), 213–246.http://dx.doi.Org/10.2969/jmsj7O222O213 Google Scholar
[Ra] Raynaud, M., Schémas en groupes de type (p,…,p). Bull Soc. Math. Fr. 102(1974), 241–280.Google Scholar
[Ta] Tate, J., p-divisiblegroups. 1967 Proc. Conf. Local Fields (Driebergen, 1966) Springer, Berlin, 1967, pp. 158–183.Google Scholar
[Zi] Zink, T., Cartiertheorie kommutativer formater Gruppen. Teubner Verlagsgesellschaft, Leipzig, 1984.Google Scholar