Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T00:57:37.149Z Has data issue: false hasContentIssue false
  • English
  • Français

k-Discreteness and k-Analytic Sets

Published online by Cambridge University Press:  20 November 2018

Ronald C. Freiwald
Ronald C. Freiwald*
Affiliation:
Washington University, St. Louis, Missouri
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

All spaces considered here are metrizable. k will always denote an infinite cardinal. The successor of k will be denoted by k+.

Of particular interest will be the Baire spaces 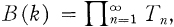where each Tn is a discrete space of cardinal k. The product topology on B(k) is the same as the topology given by the (complete) “first-difference” metric, p : p(s, t) = 1/n if Si = ti for 1 ≦ i ≦ n —1 and sn = tn. A great deal of information about these spaces can be found in [4].

A subset A of X is called k-analytic (in X) if there exist, for each t ∈ B(k), closed subsets F(t1), …, F(t1, …, tn), … of X such that

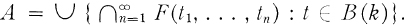
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 2 , February 1980 , pp. 331 - 341
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. El'kin, A., A-sets in complete metric spaces, Soviet Math. Dokl. 8 (1967), 874–877.Google Scholar
2. Hansell, R., Borel measurable mappings for nonseparable metric spaces, Trans. Amer. Math. Soc. 161 (1971), 145–169.Google Scholar
3. Lasnev, N., Continuous decompositions of collectively normal spaces, Soviet Math. Dokl. 188 (1967), 1069–70.Google Scholar
4. Kuratowski, K., Topology, v.1 (Academic Press, New York, 1966).Google Scholar
5. Stone, A. H., Non-separable Borel sets, Rozprawy Matematyczne 28, Warsaw (1962).Google Scholar
6. Stone, A. H., On a-discreteness and Borel isomorphism, Amer. J. Math. 85 (1963), 655–666.Google Scholar
7. Stone, A. H., Kernel constructions and Borel sets, Trans. Amer. Math. Soc. 107 (1963), 58–70.Google Scholar
8. Stone, A. H., Non-separable Borel sets, II, Gen. Top. and Appl. 2 (1972), 249–270.Google Scholar
9. Pol, R., Note on decompositions of metrizable spaces, I, Fund. Math. 95 (1977), 95–103.Google Scholar
10. Pol, R., Note on decompositions of metrizable spaces, II, Fund. Math. 100 (2) (1978), 129–143.Google Scholar
11. Preiss, D., Completely additive disjoint system of Baire sets is of bounded class, Comm. Math. Univ. Carolina. 15 (1975), 341–344.Google Scholar