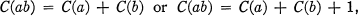Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Erdös, P.
and
Subbarao, M. V.
1972.
The Theory of Arithmetic Functions.
Vol. 251,
Issue. ,
p.
119.
Guy, Richard K.
1994.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
44.
Sándor, J.
and
Crstici, B.
2004.
Handbook of Number Theory II.
p.
179.
Guy, Richard K.
2004.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
71.
Banks, W. D.
Luca, F.
Saidak, F.
and
StĂ;nicĂ, P.
2005.
Compositions with the euler and carmichael functions.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 75,
Issue. 1,
p.
215.


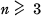 define C(n) to be the integer j such that
define C(n) to be the integer j such that 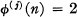 , where
, where 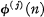 denotes the j th iterate of the Euler ø-function. Define C(l) = C(2) = 0. This function has been studied by S. S. Pillai [1], with the notation R(n) for 1 + C(n) if
denotes the j th iterate of the Euler ø-function. Define C(l) = C(2) = 0. This function has been studied by S. S. Pillai [1], with the notation R(n) for 1 + C(n) if 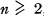 , and R(l) = 0. H. Shapiro [2] has also investigated this function, proving the basic relations
, and R(l) = 0. H. Shapiro [2] has also investigated this function, proving the basic relations