Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-20T10:39:14.514Z Has data issue: false hasContentIssue false
  • English
  • Français

Isotropic and Kähler Immersions

Published online by Cambridge University Press:  20 November 2018

Barrett O'Neill
Barrett O'Neill*
Affiliation:
University of California, Los Angeles
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

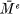Let Md and be Riemannian manifolds. We shall say that an isometric immersion ϕ: Md —> 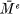is isotropic provided that all its normal curvature vectors have the same length. The class of such immersions is closed under compositions and Cartesian products. Umbilic immersions (e.g. Sd ⊂ Rd+1) are isotropic, but the converse does not hold. If M and 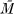are Kähler manifolds of constant holomorphic curvature, then any Kähler immersion of M in 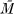is automatically isotropic (Lemma 6). We shall find the smallest co-dimension for which there exist non-trivial immersions of this type, and obtain similar results in the real constant-curvature case.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 17 , 1965 , pp. 907 - 915
Copyright
Copyright © Canadian Mathematical Society 1965

References

1. Ambrose, W., The Cartan structural equations in classical Riemannian geometry, J. Indian Math. Soc, 24 (1960), 23–76.Google Scholar
2. O'Neill, B., Umbilics of constant curvature immersions, Duke Math. J., 32 (1965), 149–160.Google Scholar