Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-25T21:09:31.875Z Has data issue: false hasContentIssue false
  • English
  • Français

Isomorphic Structure of Cesàro and Tandori Spaces

Part of: Normed linear spaces and Banach spaces; Banach lattices Linear function spaces and their duals

Published online by Cambridge University Press:  09 January 2019

Sergey V. Astashkin ,
Karol Lesnik  and
Lech Maligranda
Sergey V. Astashkin
Affiliation:
Department of Mathematics and Mechanics, Samara State University, Acad. Pavlova 1, 443011 Samara, Russia Samara State Aerospace University (SSAU), Moskovskoye shosse 34, 443086, Samara, Russia Email: [email protected]
Karol Lesnik
Affiliation:
Institute of Mathematics, Poznań University of Technology, ul. Piotrowo 3a, 60-965 Poznań, Poland Email: [email protected]
Lech Maligranda
Affiliation:
Department of Engineering Sciences and Mathematics, Luleå University of Technology, SE-971 87 Luleå, Sweden Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate the isomorphic structure of the Cesàro spaces and their duals, the Tandori spaces. The main result states that the Cesàro function space 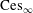$\text{Ces}_{\infty }$ and its sequence counterpart 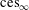$\text{ces}_{\infty }$ are isomorphic. This is rather surprising since 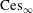$\text{Ces}_{\infty }$ (like Talagrand’s example) has no natural lattice predual. 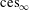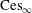We prove that $\text{ces}_{\infty }$ is not isomorphic to $\ell _{\infty }$ nor is $\text{Ces}_{\infty }$ isomorphic to the Tandori space 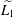$\widetilde{L_{1}}$ with the norm 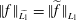$\Vert f\Vert _{\widetilde{L_{1}}}=\Vert \widetilde{f}\Vert _{L_{1}}$, where 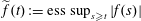$\widetilde{f}(t):=\text{ess}\,\sup _{s\geqslant t}|f(s)|$. Our investigation also involves an examination of the Schur and Dunford–Pettis properties of Cesàro and Tandori spaces. In particular, using results of Bourgain we show that a wide class of Cesàro–Marcinkiewicz and Cesàro–Lorentz spaces have the latter property.

Keywords

Cesàro and Tandori sequence spacesCesàro and Tandori function spacesCesàro operatorBanach ideal spacesymmetric spaceSchur propertyDunford–Pettis propertyisomorphism

MSC classification

Primary: 46E30: Spaces of measurable functions ($L^p$-spaces, Orlicz spaces, Köthe function spaces, Lorentz spaces, rearrangement invariant spaces, ideal spaces, etc.)
Secondary: 46B20: Geometry and structure of normed linear spaces 46B42: Banach lattices 46B45: Banach sequence spaces
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 3 , June 2019 , pp. 501 - 532
Copyright
© Canadian Mathematical Society 2018 

Footnotes

Author S. V. A. was partially supported by the Ministry of Education and Science of the Russian Federation (project 1.470.2016/1.4) and author K. L. was partially supported by the grant 04/43/DSPB/0086 from the Polish Ministry of Science and Higher Education.

References

Albiac, F. and Kalton, N. J., Topics in Banach space theory. Springer-Verlag, New York, 2006.Google Scholar
Alexiewicz, A., On Cauchy’s condensation theorem . Studia Math. 16(1957), 80–85. https://doi.org/10.4064/sm-16-1-80-85.Google Scholar
Aliprantis, C. D. and Burkinshaw, O., Positive operators. Academic Press, New York, London, 1985.Google Scholar
Astashkin, S. V. and Maligranda, L., Cesáro function spaces fail the fixed point property . Proc. Amer. Math. Soc. 136(2008), no. 12, 4289–4294. https://doi.org/10.1090/S0002-9939-08-09599-3.Google Scholar
Astashkin, S. V. and Maligranda, L., Structure of Cesáro function spaces . Indag. Math. (N.S.) 20(2009), no. 3, 329–379. https://doi.org/10.1016/S0019-3577(10)00002-9.Google Scholar
Astashkin, S. V. and Maligranda, L., Interpolation of Cesáro sequence and function spaces . Studia Math. 215(2013), no. 1, 39–69. https://doi.org/10.4064/sm215-1-4.Google Scholar
Astashkin, S. V. and Maligranda, L., Structure of Cesáro function spaces: a survey . Banach Center Publ. 102(2014), 13–40.Google Scholar
Astashkin, S. V. and Maligranda, L., L p + L ∞ and L p ∩ L ∞ are not isomorphic for all 1⩽p < ∞, p≠2 . Proc. Amer. Math. Soc.(2018), no. 5, 2181–2194. https://doi.org/10.1090/proc/13928.Google Scholar
Banach, S., Théorie des opérations linéaires. Monografje Matematyczne 1, Warszawa, 1932.Google Scholar
Bennett, G., Factorizing classical inequalities . Mem. Amer. Math. Soc. 120(1996), no. 576.Google Scholar
Bennett, C. and Sharpley, R., Interpolation of operators. Academic Press, Boston, MA, 1988.Google Scholar
Bourgain, J., New classes of  ${\mathcal{L}}^{p}$ -spaces. Lecture Notes in Math., 889. Springer-Verlag, Berlin, 1981.Google Scholar
Bourgain, J., On the Dunford–Pettis property . Proc. Amer. Math. Soc. 81(1981), no. 2, 265–272. https://doi.org/10.1090/S0002-9939-1981-0593470-8.Google Scholar
Castillo, J. M. and Gonzáles, M., On the Dunford–Pettis property in Banach spaces . Acta Univ. Carolin. Math. Phys. 35(1994), no. 2, 5–12.Google Scholar
Cembranos, P. and Mendoza, J., The Banach spaces ℓ ∞ (ℓ 1) and ℓ 1(ℓ ∞ ) are not isomorphic . J. Math. Anal. Appl. 341(2008), no. 1, 295–297. https://doi.org/10.1016/j.jmaa.2007.10.027.Google Scholar
Chu, C.-H. and Iochum, B., The Dunford–Pettis property in C∗-algebras . Studia Math. 97(1990), 59–64. https://doi.org/10.4064/sm-97-1-59-64.Google Scholar
Cui, Y. and Hudzik, H., Packing constant for Cesáro sequence spaces . Nonlinear Anal. 47(2001), 2695–2702. https://doi.org/10.1016/S0362-546X(01)00389-3.Google Scholar
Cui, Y., Meng, C., and Płuciennik, R., Banach–Saks property and property (𝛽) in Cesáro sequence spaces . Southeast Asian Bull. Math. 24(2000), 201–210.Google Scholar
Curbera, G. P. and Ricker, W. J., Abstract Cesáro spaces: integral representations . J. Math. Anal. Appl. 441(2016), no. 1, 25–44. https://doi.org/10.1016/j.jmaa.2016.03.074.Google Scholar
Curbera, G. P. and Ricker, W. J., The weak Banach–Saks property for function spaces . Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Math. RACSAM 111(2017), no. 3, 657–671. https://doi.org/10.1007/s13398-016-0317-z.Google Scholar
Delgado, O. and Soria, J., Optimal domain for the Hardy operator . J. Funct. Anal. 244(2007), no. 1, 119–133. https://doi.org/10.1016/j.jfa.2006.12.011.Google Scholar
Diestel, J., A survey of results related to the Dunford-Pettis property . Contemp. Math. 2(1980), 15–60.Google Scholar
Gogatishvili, A. and Pick, L., Discretization and anti-discretization of rearrangement-invariant norms . Publ. Mat. 47(2003), no. 2, 311–358. https://doi.org/10.5565/PUBLMAT_47203_02.Google Scholar
Goldman, M. L., Heinig, H. P., and Stepanov, V. D., On the principle of duality in Lorentz spaces . Canad. J. Math. 48(1996), no. 5, 959–979. https://doi.org/10.4153/CJM-1996-050-3.Google Scholar
Grosse-Erdmann, K.-G., The blocking technique, weighted mean operators and Hardy’s inequality . Lecture Notes in Math., 1679. Springer–Verlag, Berlin, 1998.Google Scholar
Hagler, J. and Stegall, C., Banach spaces whose duals contain complemented subspaces isomorphic to C[0, 1]∗ . J. Funct. Anal. 13(1973), 233–251. https://doi.org/10.1016/0022- 1236(73)90033-5.Google Scholar
Jagers, A. A., A note on Cesáro sequence spaces . Nieuw Arch. Wisk. 22(1974), 113–124.Google Scholar
Kalton, N., Lattice structures on Banach spaces . Mem. Amer. Math. Soc. 103(1993), no. 493.Google Scholar
Kamińska, A. and Kubiak, D., On the dual of Cesáro function space . Nonlinear Analysis 75(2012), no. 5, 2760–2773. https://doi.org/10.1016/j.na.2011.11.019.Google Scholar
Kamińska, A. and Mastyło, M., The Dunford–Pettis property for symmetric spaces . Canad. J. Math. 52(2000), no. 4, 789–803. https://doi.org/10.4153/CJM-2000-033-9.Google Scholar
Kantorovich, L. V. and Akilov, G. P., Functional analysis. Nauka, Moscow 1977 (Russian); English transl. Pergamon Press, Oxford-Elmsford, New York 1982.Google Scholar
Kerman, R., Milman, M., and Sinnamon, G., On the Brudnyĭ-Krugljak duality theory of spaces formed by the K-method of interpolation . Rev. Mat. Complut. 20(2007), no. 2, 367–389.Google Scholar
Korenblyum, B. I., Kreĭn, S. G., and Levin, B. Y., On certain nonlinear questions of the theory of singular integrals . Doklady Akad. Nauk SSSR (N.S.) 62(1948), 17–20 (Russian).Google Scholar
Krasnoselskii, M. A. and Rutickii, Y. B., Convex functions and Orlicz spaces. Noordhoff, Groningen, 1961.Google Scholar
Krein, S. G., Petunin, Y. I., and Semenov, E. M., Interpolation of linear operators. Amer. Math. Soc., Providence, RI, 1982.Google Scholar
Leśnik, K. and Maligranda, L., On abstract Cesáro spaces . Duality. J. Math. Anal. Appl. 424(2015), no. 2, 932–951. https://doi.org/10.1016/j.jmaa.2014.11.023.Google Scholar
Leśnik, K. and Maligranda, L., Abstract Cesáro spaces . Optimal range. Integral Equations Operator Theory 81(2015), no. 2, 227–235. https://doi.org/10.1007/s00020-014-2203-4.Google Scholar
Leśnik, K. and Maligranda, L., Interpolation of abstract Cesáro, Copson and Tandori spaces . Indag. Math. (N.S.) 27(2016), no. 3, 764–785. https://doi.org/10.1016/j.indag.2016.01.009.Google Scholar
Leung, D. H., Isomorphism of certain weak L p spaces . Studia Math. 104(1993), no. 2, 151–160. https://doi.org/10.4064/sm-104-2-151-160.Google Scholar
Lin, P.-K., Köthe–Bochner function spaces. Birkhäuser, Boston, 2004.Google Scholar
Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces, I. Sequence spaces. Springer–Verlag, Berlin, 1977.Google Scholar
Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces, II. Function spaces. Springer–Verlag, Berlin, 1979.Google Scholar
Lotz, H. P., The Radon–Nikodym property in Banach lattices. Univ. of Illinois, Urbana-Champaign, preprint, 1975.Google Scholar
Luxemburg, W. A. J. and Zaanen, A. C., Some examples of normed Köthe spaces . Math. Ann. 162(1966), 337–350. https://doi.org/10.1007/BF01369107.Google Scholar
Maligranda, L., Indices and interpolation . Dissertationes Math. (Rozprawy Mat.) 234(1985), 1–49.Google Scholar
Maligranda, L., Orlicz spaces and interpolation . Seminars in Mathematics 5, University of Campinas, Campinas, 1989.Google Scholar
Maligranda, L., Petrot, N., and Suantai, S., On the James constant and B-convexity of Cesáro and Cesáro–Orlicz sequence spaces . J. Math. Anal. Appl. 326(2007), no. 1, 312–331. https://doi.org/10.1016/j.jmaa.2006.02.085.Google Scholar
Mastyło, M. and Sinnamon, G., A Calderón couple of down spaces . J. Funct. Anal. 240(2006), no. 1, 192–225. https://doi.org/10.1016/j.jfa.2006.05.007.Google Scholar
Nekvinda, A. and Pick, L., Optimal estimates for the Hardy averaging operator . Math. Nachr. 283(2010), no. 2, 262–271. https://doi.org/10.1002/mana.200711155.Google Scholar
Okada, S., Ricker, W. J., and Sánchez Pérez, E., Optimal domain and integral extension of operators acting in function spaces. Birkhäuser–Verlag, Basel, 2008.Google Scholar
Pełczyński, A., On the isomorphism of the spaces m and M . Bull. Acad. Polon. Sci. Sér. Sci. Math. Astr. Phys. 6(1958), 695–696.Google Scholar
Pełczyński, A., Projections in certain Banach spaces . Studia Math. 19(1960), 209–228. https://doi.org/10.4064/sm-19-2-209-228.Google Scholar
Rutickiĭ, J. B., Operators with homogeneous kernels . Sibirsk. Mat. Zh. 21(1980), no. 1, 153–160; English transl. in: Siberian Math. J. 21 (1980), no. 1, 113–118.Google Scholar
Sinnamon, G., Spaces defined by the level function and their duals . Studia Math. 111(1994), no. 1, 19–52. https://doi.org/10.4064/sm-111-1-19-52.Google Scholar
Sinnamon, G., The level functions in rearrangement invariant spaces . Publ. Mat. 45(2001), no. 1, 175–198. https://doi.org/10.5565/PUBLMAT_45101_08.Google Scholar
Sinnamon, G., Monotonicity in Banach function spaces. In: Nonlinear analysis, function spaces and applications, NAFSA 8, vol. 8, Czech. Acad. Sci., Prague 2007, 204–240.Google Scholar
Talagrand, M., Dual Banach lattices and Banach lattices with the Radon-Nikodym property . Israel J. Math. 38(1981), 46–50. https://doi.org/10.1007/BF02761847.Google Scholar
Tandori, K., Über einen speziellen Banachschen Raum . Publ. Math. Debrecen 3(1954), 263–268. 1955.Google Scholar
Wnuk, W., Banach lattices with properties of the Schur type–a survey . Confer. Sem. Mat. Univ. Bari 249(1993), 1–25.Google Scholar
Wnuk, W., Banach lattices with order continuous norms. Polish Scientific Publishers PWN, Warszawa, 1999.Google Scholar