Recently A. Gutek, D. Hart, J. Jamison and M. Rajagopalan have obtained many significiant results concerning shift operators on Banach spaces. Using a result of Holsztynski they classify isometric shift operators on C(X) for any compact Hausdorff space X into two (not necessarily disjoint) classes. If there exists an isometric shift operator T: C(X) → C(X) of type II, they show that X is necessarily separable. In case T is of type I, they exhibit a paticular infinite countable set 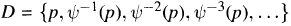of isolated points in X. Under the additional assumption that the linear functional Γ carrying f ∊ C(X) to Tf(p) ∊ 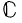is identically zero, they show that D is dense in X. They raise the question whether D will still be dense in X even when Γ ≠ 0. In this paper we give a negative answer to this question. In fact, given any integer l ≥ 1, we construct an example of an isometric shift operator T: C(X) —> C(X) of type I with X \ 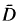having exactly / elements, where 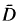is the closure of D in X.