Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T00:53:05.155Z Has data issue: false hasContentIssue false
  • English
  • Français

Isometric Characterizations of ℓnp Spaces

Published online by Cambridge University Press:  20 November 2018

Ryszard Komorowski
Ryszard Komorowski*
Affiliation:
Department of Mathematics The University of Alberta Edmonton, Alberta T6G 2G1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The paper establishes some characterizations of 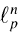spaces in terms of p-summing or p-nuclear norms of the identity operator on the given space E.

In particular, for an n-dimensional Banach space E and I ≤ p < 2, E is isometric to 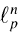if and only if πp(E*) ≥ n1/p and E* has cotype p' with the constant one.

Furthermore, 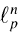spaces are characterized by inequalities for p-summing norms of operators related to the John's ellipsoid of maximal volume contained in the unit ball of E.

Keywords

46B0446B15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 46 , Issue 3 , 01 June 1994 , pp. 574 - 585
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. Bourgain, J. and Tzafriri, L., Invertibility of ‘large ‘ submatrices with applications to the geometry ofBanach spaces and harmonic analysis, Israel J. Math. 57(1987), 137–224.Google Scholar
2. Deschaseaux, J. P., Une caractérisation de certains espaces vectoriel normes de dimension finie par leur constante de Macphail,C R. Acad. Sci. Paris (A/B) 276(1973), 1349–1351.Google Scholar
3. Figiel, T. and Johnson, W. B., Large subspaces of l^ and estimates of the Gordon-Lewis constant, Israel J. Math. 37(1980), 92–112.Google Scholar
4. Garling, D. J. H., Operators with large trace and characterization of l^, Proc. Cambridge Philos. Soc. 76(1974), 413–414.Google Scholar
5. Garling, D. J. H., Absolutely p-summing operators in Hilbert spaces, Studia Math. 38(1970), 319–321.Google Scholar
6. Lewis, D. R., Finite dimensional subspaces ofLp, Studia. Math. 63(1978), 207–212.Google Scholar
7. Nachbin, L., A theorem of the Hahn-Banach type for linear transformations, Trans. Amer. Math. Soc. 68(1950), 28–46.Google Scholar
8. Pietsch, A., Operator Ideals, VEB Deutscher Verlag, Berlin, North-Holland, Amsterdam, 1978.Google Scholar
9. Tomczak-Jaegermann, N., Banach-Mazur distance and finite dimensional operator ideals, Pitman Monographs and Surveys in Pure and App. Math. Longman Sci. & Tech. Harlow & J. Wiley, New York, 1989.Google Scholar