Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-11T02:06:06.579Z Has data issue: false hasContentIssue false
  • English
  • Français

Invertibility Threshold for Nevanlinna Quotient Algebras

Part of: Spaces and algebras of analytic functions Function theory on the disc

Published online by Cambridge University Press:  10 September 2021

Artur Nicolau  and
Pascal J. Thomas
Artur Nicolau*
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, 08193 Barcelona, Spain
Pascal J. Thomas
Affiliation:
Institut de Mathématiques de Toulouse, UMR5219, Université de Toulouse, CNRS, UPS IMT, F-31062 Toulouse Cedex 9, France e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

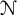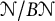Let $\mathcal {N}$ be the Nevanlinna class, and let B be a Blaschke product. It is shown that the natural invertibility criterion in the quotient algebra $\mathcal {N} / B \mathcal {N}$ , that is, 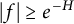$|f| \ge e^{-H} $ on the set 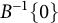$B^{-1}\{0\}$ for some positive harmonic function H, holds if and only if the function 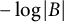$- \log |B|$ has a harmonic majorant on the set 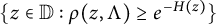$\{z\in \mathbb {D}:\rho (z,\Lambda )\geq e^{-H(z)}\}$ , at least for large enough functions H. We also study the corresponding class of positive harmonic functions H on the unit disc such that the latter condition holds. We also discuss the analogous invertibility problem in quotients of the Smirnov class.

MSC classification

Primary: 30H15: Nevanlinna class and Smirnov class
Secondary: 30H80: Corona theorems 30J10: Blaschke products
Type
Article
Information
Canadian Journal of Mathematics , Volume 75 , Issue 1 , February 2023 , pp. 225 - 244
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

First author is supported by the Generalitat de Catalunya (grant 2017 SGR 395) and the Spanish Ministerio de Ciencia e Innovación (project MTM2017-85666-P).

References

Borichev, A., Generalized Carleson–Newman inner functions. Math. Z. 275(2013), nos. 3–4, 1197–1206.Google Scholar
Borichev, A., Nicolau, A., and Thomas, P., Weak embedding property, inner functions and entropy. Math. Ann. 368(2017), no. 3–4, 987–1015.Google Scholar
Carleson, L., An interpolation problem for bounded analytic functions. Amer. J. Math. 80(1958), 921–930.CrossRefGoogle Scholar
Carleson, L., Interpolations by bounded analytic functions and the corona problem. Ann. Math. 76(1962), no. 2, 547–559.Google Scholar
Garnett, J. B., Bounded analytic functions. Revised 1st ed., Graduate Texts in Mathematics, 236, Springer, New York, 2007.Google Scholar
Gorkin, P., Mortini, R., and Nikolski, N., Norm controlled inversions and a corona theorem for ${H}^{\infty }$ -quotient algebras. J. Funct. Anal. 255(2008), 854–876.CrossRefGoogle Scholar
Hartmann, A., Massaneda, X., Nicolau, A., and Thomas, P., Interpolation in the Nevanlinna and Smirnov classes and harmonic majorants. J. Funct. Anal. 217(2004), no. 1, 1–37.CrossRefGoogle Scholar
Martin, R., On the ideal structure of the Nevanlinna class. Proc. Amer. Math. Soc. 114(1992), no. 1, 135–143.CrossRefGoogle Scholar
Massaneda, X., Nicolau, A., and Thomas, P., The Corona property of Nevanlinna quotient algebras and interpolating sequences. J. Funct. Anal. 276(2019), no. 8, 2636–2661.Google Scholar
Mortini, R., Zur Idealstruktur von Unterringen der Nevanlinna–Klasse N. In: Travaux mathématiques, I, Sém. Math. Luxembourg, Centre Univ. Luxembourg, Luxembourg, 1989, pp. 81–91.Google Scholar
Nikolski, N. and Vasyunin, V., Invertibility threshold for the $\ {H}^{\infty }$ -trace algebra and the efficient inversion of matrices. Algebra i Analiz 23(2011), no. 1, 87–110.Google Scholar